Prima di tutto presentiamo gli elementi fondamentali della meccanica classica così come sono trattati da un "manuale" recente, scelto più o meno caso. Si suppone che qualsiasi manuale raccolga, in modo coerente e corretto, le definizioni e le leggi essenziali ad una prima comprensione della teoria. In seguito commenteremo i singoli enunciati del manuale allo scopo di mostrare che la presentazione "corretta" di una teoria non è univoca, ma implica delle scelte soggettive legate alla formazione scientifica dell'autore, al "linguaggio" (in senso lato) e alla visione corrente del mondo fisico propri dell'ambiente in cui l'autore opera.

Presentiamo quindi una sintesi dei primi capitoli del "Manuale di Fisica", di Javorskij e Detlaf (Ed. MIR, Mosca, 1977). Il manuale, complessivamente di circa 750 pagine, contiene i Fondamenti della meccanica classica come Parte Prima, suddivisa nei seguenti argomenti: Cinematica del punto materiale e del solido perfetto, Dinamica del moto di traslazione, Lavoro ed energia meccanica, Dinamica del moto di rotazione, Elementi di meccanica analitica, Oscillazioni meccaniche. Le parti successive riguardano: Elementi di termodinamica e fisica molecolare, Elementi di idrodinamica, Elettricità e Magnetismo, Moti ondulatori, Fisica atomica e nucleare.

Definizione di meccanica: studio della variazione della disposizione reciproca dei corpi e delle loro parti nello spazio e nel tempo.

Definizione di corpi: sistemi macroscopici, formati da un gran numero di particelle o di atomi, le cui dimensioni sono molto più grandi delle distanze intermolecolari. La meccanica non si occupa della struttura interna dei corpi, ma li considera come punti materiali o come solidi perfetti.

Definizione di punto materiale: corpo le cui dimensioni spaziali non hanno alcuna rilevanza ai fini del suo movimento. Un sistema meccanico può essere costituito da un insieme di punti materiali.

Definizione di solido perfetto: corpo tale che la distanza tra due suoi componenti qualsiasi resti costante nel tempo.

Suddivisione della meccanica: la meccanica comprende la statica (studio delle condizioni per l'equilibrio meccanico), la cinematica (studio del movimento indipendentemente dalle cause che lo producono) e dinamica (studio del movimento come effetto dell'interazione tra i corpi).

Definizione di sistema di riferimento: un sistema di riferimento è un corpo solido perfetto, reale o astratto, rispetto al quale si studia il moto degli altri corpi. Al sistema di riferimento è associato un sistema di coordinate spaziali più un orologio. Il moto del corpo sarà allora descritto da variazioni delle coordinate nel tempo. In linguaggio matematico: q₁=q₁(t), q₂=q₂(t), ecc., se q₁, q₂, ... sono le coordinate spaziali e t è il tempo. La traiettoria seguita dal punto nel suo movimento è fissata da una equazione del tipo f(q₁,q₂,...)=0, che si trova eliminando il tempo t dalle equazioni q₁=q₁(t), q₂=q₂(t), ecc. . I valori delle coordinate e, quindi, la forma della traiettoria dipendono dalla scelta del sistema di riferimento. Una scelta ragionevole per studiare il moto nell'usuale spazio a 3 dimensioni è la terna di coordinate ortogonali cartesiane x,y,z, in modo che la posizione di un generico punto materiale è fissata dal vettore r = (x,y,z), che è funzione del tempo, r = r(t). In alcuni casi può essere più conveniente la scelta di un sistema di coordinate sferiche o cilindriche. Se il sistema meccanico è vincolato ad un sottospazio (moto in un piano, o su una superficie curva assegnata, ecc.) si introducono delle coordinate ad hoc, dette coordinate generalizzate, che rappresentano i gradi di libertà effettivi del sistema stesso.

Definizione di velocità (istantanea): la velocità di un punto materiale è data dal rapporto

è un vettore orientato secondo la tangente alla traiettoria. Il modulo è la derivata dello spazio percorso lungo la traiettoria stessa, v=ds/dt. Per il moto su un piano può essere utile scomporre la velocità in una parte radiale e una parte angolare, utilizzando coordinate polari.

Definizione di velocità media: grandezza scalare pari al rapporto tra spazio percorso e intervallo di tempo corrispondente

Nel limite in cui l'intervallo di tempo diventa infinitesimo, la velocità media coincide con il modulo della velocità istantanea.

Definizione di accelerazione: l'accelerazione, che caratterizza le variazioni di velocità nel tempo, è data dal rapporto

Di nuovo, nel caso, di un moto in un piano, può essere conveniente introdurre una accelerazione radiale e una accelerazione angolare. Oppure, lungo la traiettoria si possono individuare le accelerazioni normale e tangenziale (perpendicolare e parallela, punto per punto, alla traiettoria stessa).

Definizione di moto uniforme e moto uniformemente accelerato: si ha moto uniforme quando v=costante. Allora a=0 e s=v(t-t₀), se t₀ è un istante iniziale arbitrario. Si ottiene invece moto uniformemente accelerato quando a=costante. Allora v=v₀+a(t-t₀), con v₀ velocità iniziale al tempo t₀, e lo spazio percorso aumenta con il quadrato del tempo.

Moto di traslazione e moto di rotazione: nel caso dei solidi perfetti bisogna distinguere, nel movimento complessivo del corpo, un moto di pura traslazione, in cui tutte le traiettorie delle singole parti del corpo sono parallele tra loro, e un moto di rotazione, in cui tutte le parti del corpo compiono un moto circolare attorno ad un certo asse. L'asse di rotazione può pure variare nel tempo. Il moto di rotazione è caratterizzato dalla velocità angolare (rapporto di angoli e tempo).

Prima legge di Newton: tutti i punti materiali conservano il loro stato di riposo o di moto rettilineo uniforme fino a quando l 'azione di altri corpi non li fa uscire da tale stato.

Questa legge è detta principio di inerzia e il moto di un punto materiale non sottoposto a forze esterne si chiama inerziale. Un sistema di riferimento in cui vale il principio di inerzia è detto sistema inerziale.

Concetto di forza: la forza è una grandezza vettoriale che misura l'azione meccanica esercitata su un punto materiale e su un corpo da un altro corpo o campo.

Dal principio di inerzia segue che l'interazione mutua tra i corpi è la causa della variazione del loro stato di moto. Tale interazione provoca, inoltre, la deformazione dei corpi. La misura della deformazione di uno stesso corpo elastico permette di confrontare le forze tra loro e stabilire campioni di misura.

Nel manuale, seguono ulteriori specificazioni del concetto di forza: regola di composizione, la risultante delle forze, la linea d'azione, le forze interne ed esterne, i sistemi isolati, le forze vincolari e gli attriti.

Concetto di massa: la massa di un corpo è una grandezza fisica che tiene conto delle proprietà di inerzia e di gravitazione del corpo stesso. La massa è una grandezza scalare per cui valgono le seguenti proprietà: è additiva (la massa di un corpo scomposto in parti arbitrarie è la somma delle masse di ciascuna parte), non dipende dalla velocità del corpo e, per un sistema isolato, si conserva (non dipende la tempo).

La massa che compare nella II legge di Newton caratterizza le proprietà inerziali e viene detta massa inerziale. La massa che compare nella legge di attrazione universale caratterizza le proprietà gravitazionali e viene detta massa gravitazionale. Si verifica che la massa inerziale e la massa gravitazionale sono uguali. Ciò permette di misurare la massa con semplici bilance.

Per un corpo esteso si può definire una densità di massa, in modo che la massa totale sia l'integrale della densità eseguito sul volume occupato dal corpo stesso. Per un corpo omogeneo la massa totale è il prodotto della densità per il volume.

Per un sistema di punti materiali si può definire un centro di massa (o centro di inerzia) dato dal raggio vettore

.

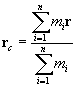Concetto di quantità di moto: la quantità di moto di un punto materiale è il vettore definito dal prodotto della massa per la velocità

.

Nel caso di un sistema di punti materiali basta sommare le singole quantità di moto dei componenti per ottenere quella totale.

La seconda legge di Newton: la variazione elementare della quantità di moto di un punto materiale è uguale all'impulso elementare della forza applicata

.

Oppure

.

L'impulso della forza per un intervallo finito di tempo è l'integrale dell'impulso elementare Fdt nello stesso intervallo di tempo. Se la massa del corpo è costante, la seconda legge può essere scritta nella forma

.

Ovvero, l'accelerazione di un punto materiale ha la stessa direzione della forza ad esso applicata, è proporzionale a tale forza e inversamente proporzionale alla sua massa. L'equazione che dà la relazione tra l'accelerazione e la forza è anche detta equazione differenziale del moto.

Per la seconda legge di Newton vale un principio di sovrapposizione: se più forze agiscono simultaneamente su un punto materiale, ognuna di esse comunicherà una accelerazione che è determinata dalla seconda legge di Newton, come se le altre forze non esistessero. L'accelerazione totale è fissata dalla somma (risultante) delle forze.

Terza legge di Newton: Le azioni che due punti materiali esercitano l'uno sull'altro sono uguali in modulo e dirette in senso opposto:

.

Legge di conservazione della quantità di moto: La quantità di moto di un sistema isolato è costante. Questa è una delle leggi fondamentali della natura che trova la sua origine nella omogeneità dello spazio. La legge di conservazione della quantità di moto mostra che l'interazione tra i corpi che compongono un sistema chiuso si riduce ad uno scambio di quantità di moto fra questi corpi, ma non può variare il moto del sistema nel suo insieme intero, qualunque sia il tipo di interazione.

Legge fondamentale del moto di traslazione: la derivata temporale della quantità di moto di un sistema di punti materiali, in un sistema di riferimento inerziale, è uguale alla risultante delle forze esterne applicate al sistema. In forma matematica:

dove a_c è l'accelerazione del centro di massa. Per questo motivo, il moto di un corpo esteso, per quanto riguarda la sua traslazione, può essere ridotto al moto di un punto materiale posto nel suo centro di massa e su cui agisce la risultante delle forze esterne.

Il principio di relatività (in meccanica classica): La relazione esistente tra le coordinate e i tempi, relativi a due sistemi di riferimento inerziali arbitrari, è data dalle trasformazioni di Galileo:

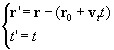
dove v_t è la velocità relativa, costante, dei due sistemi di riferimento e r₀ è la distanza tra le origini dei due sistemi al tempo t₀. La seconda relazione esprime il carattere assoluto del tempo in meccanica classica, il fatto cioè che il tempo scorre in maniera identica in tutti i sistemi di riferimento inerziali.

Le trasformazioni di Galileo sono tali che l'accelerazione di un punto materiale qualsiasi soggetto ad una data forza è la stessa in tutti i sistemi di riferimento inerziali:

e quindi F'=F.

Le leggi del moto sono quindi invarianti rispetto alle trasformazioni di Galileo.

Moto in sistemi non inerziali: benché le leggi di Newton siano valide solamente per il moto nei sistemi inerziali (il principio di inerzia vale solo nei sistemi inerziali per definizione), la II legge può essere utilizzata formalmente anche per un sistema non inerziale di cui si conosca l'accelerazione rispetto ad uno inerziale. In tal caso, infatti, la trasformazione dell'accelerazione dal sistema inerziale a quello non inerziale introduce uno o più termini aggiuntivi, dovuti al moto accelerato di traslazione del sistema o alla rotazione degli assi. Moltiplicando tali accelerazioni per la massa del corpo di cui si studia il moto, si ottengono delle grandezze aventi le dimensioni di forze. La II legge, nel sistema non inerziale, è quindi formalmente identica a quella valida per il sistema inerziale, salvo includere le forze "fittizie" derivanti dal moto accelerato del sistema di riferimento (forza fittizia di trascinamento, forza centrifuga, forza di Coriolis).

La legge di attrazione universale: Fra tutte le coppie di punti materiali agiscono forze di mutua attrazione che sono proporzionali alla massa di questi punti ed inversamente proporzionali al quadrato delle loro distanza:

,

dove u₁₂ è un vettore unitario nella direzione della congiungente i due punti. Il valore numerico della costante dipende dalle unità di misura utilizzate per masse, distanze e forze.

La forza di attrazione ha la stessa forma anche per due corpi sferici; in tal caso la distanza che appare nell'espressione della forza è la distanza tra i due centri. Così pure è valida per un corpo di forma qualsiasi attratto da una sfera, nel caso in cui il raggio della sfera sia molto maggiore delle dimensioni del corpo in questione. Questo è anche il caso degli oggetti posti in prossimità della superficie terrestre, per i quali vale

dove M_T e R_T sono, rispettivamente, la massa e il raggio della terra. La nuova costante g ha le dimensioni di una accelerazione (distanza su tempo al quadrato) e viene chiamata accelerazione di gravità. Si noti che l'accelerazione di gravità è la stessa per tutti i corpi. Il fatto che un corpo qualsiasi cade sulla superficie della terra con accelerazione g segue dall'equivalenza della massa gravitazionale e della massa inerziale; solo in tal caso infatti, inserendo l' espressione della forza di gravità nella seconda legge di Newton, la massa scompare dal risultato.

Energia: si chiama energia quella grandezza fisica che permette di valutare in maniera univoca le diverse forme di moto. L'energia è una grandezza scalare. Per poter dare una valutazione quantitativa delle forme di moto qualitativamente diverse che si trovano nella fisica, si introducono le diverse forme di energia: meccanica, interna, elettromagnetica, nucleare, ecc.

Legge di conservazione dell'energia: quali che siano i processi che avvengono in un sistema isolato, la sua energia totale non cambia nel tempo.

Questa legge è una delle più importanti della natura ed è conseguenza della omogeneità del tempo.

Lavoro: il lavoro elementare eseguito da una forza è dato dal prodotto scalare della forza stessa per lo spostamento infinitesimo del suo punto di applicazione:

.

Il lavoro compiuto su un percorso tra due punti generici A e B è l'integrale del lavoro elementari lungo lo stesso percorso.

.

L'integrale può dipendere, in generale, dalla scelta del percorso tra i due punti assegnati. In tal caso il lavoro elementare non è un differenziale esatto. Se invece il lavoro elementare è un differenziale esatto, allora il lavoro non dipende dalla scelta del percorso (dL=dL) e la forza è detta forza potenziale. Nel caso di forze che non dipendono esplicitamente dal tempo, la forza potenziale è detta anche conservativa.

La potenza è il lavoro eseguito nell'unità di tempo

.

Forze conservative ed energia potenziale: nel caso di forze che non dipendono dal tempo, la condizione che esse siano conservative è equivalente ad assumere che il lavoro eseguito lungo un percorso chiuso qualsiasi è identicamente nullo:

.

Affinché si realizzi questa condizione è necessario e sufficiente che l'integrando sia il differenziale esatto di una certa funzione scalare delle coordinate, nella forma:

,

dove il segno meno è stato introdotto per convenzione. La quantità U(x,y,z) così definita viene chiamata energia potenziale. Dall'espressione precedente segue anche:

.

Così, il lavoro svolto da una forza conservativa spostando un punto materiale da A a B vale

.

L'energia potenziale è la forma di energia che dipende dalla configurazione del sistema, cioè dalla disposizione reciproca delle particelle del sistema e dalla loro posizione rispetto ad un campo di forze esterne. Tale energia è misurata tramite il lavoro che le forze conservative (interne ed esterne) compiono nel passaggio da una configurazione assegnata ad una configurazione di riferimento, a cui si associa arbitrariamente energia potenziale nulla (U(B)=0, nella formula precedente, se B è la configurazione di riferimento).

Energia cinetica: l'energia cinetica è il lavoro che un corpo può compiere quando il suo moto sia frenato fino all'arresto totale. A partire dalle leggi di Newton si mostra che tale lavoro, nel caso di un singolo punto materiale, è dato da

.

Energia meccanica: l'energia meccanica di un punto materiale è data dalla somma dell'energia cinetica e dell'energia potenziale, E=T+U. Per un sistema di punti materiali, l'energia totale è la somma delle energie dei singoli punti.

Se tutte le forze che agiscono sul sistema sono conservative, l'energia meccanica è costante nel tempo (principio di conservazione dell 'energia meccanica).

Un sistema è detto, invece, dissipativo quando la sua energia meccanica diminuisce nel tempo in conseguenza della trasformazione in altre forme (non meccaniche) di energia (ad esempio, calore).

Coordinate generalizzate: sono i parametri indipendenti q₁,q₂,...,q_n che determinano completamente la configurazione di un sistema meccanico, cioè la posizione di tutti i suoi punti rispetto ad un dato sistema di riferimento. Per un sistema di punti materiali liberi si possono prendere semplicemente le coordinate cartesiane x,y,z di ciascun punto. Il sistema può essere sottoposto a vincoli, in modo che il moto dei punti sia limitato a un sottospazio dell'usuale spazio tridimensionale (ad esempio un moto su un piano, su una sfera, ecc.). I vincoli bilaterali indipendenti dal tempo possono essere espressi tramite un certo numero di equazioni del tipo

.

I vincoli sono detti olonomi se le equazioni che li descrivono non contengono le derivate rispetto al tempo delle coordinate o possono essere ridotte in tale forma mediante integrazione. Un sistema meccanico sottoposto a soli vincoli olonomi è detto sistema olonomo. Per un tale sistema si definiscono tante coordinate generalizzate quanti sono i gradi di libertà (numero dei possibili moti indipendenti, compatibili con i vincoli). Ogni variazione infinitesima della configurazione del sistema, compatibile con i vincoli esterni all'istante t, è detto spostamento virtuale e può essere scritto nella forma

.

Allora, il lavoro elementare compiuto durante uno spostamento virtuale dalle forze che agiscono su un sistema olonomo con s gradi di libertà vale

,

dove Q_i è detta forza generalizzata. Se i vincoli sono privi di attrito (o ideali) le forze generalizzate sono fissate unicamente dalle forze applicate (non vincolari), i vincoli essendo già implicitamente inclusi tramite le definizioni delle coordinate generalizzate. Se, inoltre, le forze applicate sono conservative, le forze generalizzate possono essere espresse tramite l'energia potenziale del sistema

.

Funzione di Lagrange: la differenza dell'energia cinetica e dell'energia potenziale del sistema, espresse in termini delle coordinate generalizzate, è detta funzione di Lagrange, o lagrangiana. Può essere scritta come

,

dove il punto sopra le variabili indica la derivazione rispetto al tempo. In questo caso la lettera q indica l'insieme delle coordinate generalizzate.

Equazione di Lagrange: si può dimostrare, a partire dalle leggi già enunciate, che il moto di un sistema olonomo soggetto a forze conservative obbedisce all'equazione

,

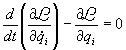detta equazione di Lagrange. Tale equazione può essere generalizzata al caso di sistemi olonomi qualsiasi, introducendo potenziali generalizzati e funzioni dissipative. La soluzione dell'equazione di Lagrange per un dato sistema è equivalente all'uso delle tre leggi di Newton [un'altra formulazione equivalente consiste nell'introdurre la funzione di Hamilton (hamiltoniana) e scrivere le equazioni canoniche di Hamilton; ma non discutiamo qui questo problema].

Princìpi variazionali: le equazioni del moto di un sistema meccanico o le sue condizioni di equilibrio possono essere ottenute come risultato di certi procedimenti generali chiamati princìpi variazionali della meccanica. I princìpi variazionali mostrano in che cosa lo stato reale di un sistema meccanico differisca da tutti gli altri suoi possibili stati virtuali compatibili con i vincoli impostigli. Uno di essi è il principio di minima azione: tra tutti i moti virtuali ammessi per il passaggio di un sistema meccanico da una configurazione iniziale all'istante t_i ad una configurazione finale all'istante t_f (definite da due insiemi di coordinate generalizzate q_i e q_f ), il moto reale del sistema avviene in modo che l' integrale

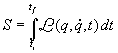
assuma il valore minimo. La funzione S è detta azione. Il principio di minima azione vale per i sistemi olonomi.

Integrali del moto e leggi di conservazione: a partire dall'equazione di Lagrange è possibile discutere , in maniera diretta, il problema delle quantità conservate. Infatti, le soluzioni dell'equazione di Lagrange per un sistema meccanico a s gradi di libertà, contengono 2s costanti arbitrarie associate alle posizioni e alle velocità iniziali dei punti del sistema. Possono allora essere scritte nella forma

con i=1,2,...,s. Da queste equazioni è possibile eliminare il tempo e quindi trovare, per ogni sistema meccanico, delle funzioni delle coordinate e delle velocità generalizzate che restano costanti nel tempo. Queste funzioni sono dette integrali del moto. La ricerca di tali integrali del moto è il compito principale della meccanica. Tra questi integrali del moto ve ne sono alcuni più importanti, la cui costanza nel tempo deriva da proprietà fondamentali dello spazio e del tempo. Ad esempio, si può facilmente dimostrare che la conservazione dell'energia totale, E=T+U=costante, è ottenuta dall'equazione di Lagrange imponendo che la lagrangiana non dipenda esplicitamente dal tempo (¶ L/¶ t = 0). Ciò equivale a dire che le equazioni del moto non dipendono dalla scelta dell'origine dei tempi (omogeneità del tempo). L'energia E è dunque un integrale del moto. In modo analogo si può verificare che l'equazione di Lagrange implica la conservazione della quantità di moto per un sistema isolato, qualora si assuma che le proprietà meccaniche di un sistema isolato non cambino per effetto di una traslazione globale (omogeneità dello spazio). L'isotropia dello spazio (indipendenza del comportamento meccanico dalla scelta dell'orientazione degli assi del sistema di riferimento) conduce infine alla conservazione di un'altra quantità, detta momento angolare, o momento della quantità di moto. Così, ogni sistema meccanico isolato ammette almeno sette integrali del moto (sette leggi di conservazione in forma scalare): una per l'energia, tre per le componenti della quantità di moto e tre per le componenti del momento angolare.

Ci fermiamo qui con la sintesi del manuale di fisica. Le definizioni e le leggi sopra elencate sono sufficienti ad avere una visione ragionevole di quali siano i contenuti della meccanica. Abbiamo volutamente sfrondato alcune parti che non aggiungono concetti veramente nuovi, ma che sono piuttosto delle generalizzazioni di quanto già esposto. Ad esempio, il problema del moto di rotazione dei sistemi di punti materiali e dei corpi solidi (velocità angolare, momento d'inerzia, momento della forza, momento angolare e legge fondamentale per le rotazioni), il problema degli urti e la trattazione delle forze d'attrito.

Il manuale è volutamente sintetico; esso esclude, in particolare, riferimenti allo sviluppo storico dei concetti, al significato di ciascuna definizione e legge nell'ambito della fisica moderna e a eventuali conflitti con altre teorie. Il manuale è pensato come una struttura minima, una raccolta di concetti assodati, un bagaglio utile per chi ha bisogno di teorie fisiche ad uso professionale (didattico o di ricerca). Volendo qui discutere di storia e di metodo, il passo successivo sarà la rilettura critica dello stesso manuale.