[ indietro ] [ indice ] [ avanti ]
III
Una rilettura critica del manuale
1. Nozioni preliminari
Definizione di meccanica: studio della variazione della
disposizione reciproca dei corpi e delle loro parti nello spazio e nel
tempo.
Questa prima parte di nozioni preliminari deve contenere
necessariamente alcuni concetti dati per noti a priori o comunque legati ad
una visione intuitiva che sostituisca ulteriori specificazioni. Così la
"variazione della disposizione reciproca dei corpi" è data intuitivamente. In
effetti, si tratta di un concetto primitivo ben definito, associato alla
nostra percezione della realtà (il movimento muscolare, il movimento degli
occhi che seguono un oggetto in moto, lo spostamento di una sorgente sonora
rispetto alle nostre orecchie, ecc.). Tutto ciò non richiede una definizione
preliminare di coordinate o di orologi; questo introdurrebbe una circolarità
nel ragionamento. L'importante, quando si definisce l'oggetto dello studio
della fisica, è capirsi su basi intuitive, intendendosi su cosa si sta
parlando. Nulla di meglio quindi che utilizzare le percezioni comuni a tutti
gli osservatori.
Lo stesso vale per i concetti di spazio e tempo. Un manuale
di fisica non si pone il problema di cosa siano spazio e tempo in sé;
piuttosto fornirà dei metodi operativi per la misura di spazio e tempo, intesi
in senso fisico. Ciò non toglie che la conoscenza di leggi fisiche, che
discendono da queste procedure operative, non possa modificare i concetti di
spazio e tempo in un contesto più generale che include la filosofia, la
psicologia, ecc.
Definizione di corpi: sistemi macroscopici, formati da un
gran numero di particelle o di atomi, le cui dimensioni sono molto più grandi
delle distanze intermolecolari.
La definizione di corpi data da questo manuale presuppone la
conoscenza della struttura della materia in termini di atomi e molecole. Tale
conoscenza è relativamente recente, sicuramente posteriore alla formulazione
della meccanica classica. è quindi naturale pensare che il concetto di corpo,
accettato come nozione preliminare della meccanica, possa anche essere
introdotto su basi puramente intuitive, senza riferimenti alla struttura
interna della materia. Di nuovo, si tratta di capirsi su quale sia l'oggetto
del discorso.
Si noti anche che la definizione scelta da questo manuale
appare alquanto restrittiva e, per certi versi, fuorviante. La meccanica
infatti può ben essere applicata anche all'ambito microscopico, per lo studio
del moto di singole particelle (microscopiche) anche su scala atomica. Su
questa scala la teoria corretta è la meccanica quantistica (pur sempre
"meccanica"). Tuttavia, la meccanica classica newtoniana, a cui la meccanica
quantistica si riduce in opportuni limiti, rimane in grado di predire e
interpretare il comportamento di singole particelle e atomi, come il moto di
singoli elettroni in campi magnetici ed elettrici, il moto degli atomi di un
gas, le collisioni tra particelle alfa e nuclei atomici, e molti altri
fenomeni.
La meccanica non si occupa della struttura interna dei corpi,
ma li considera come punti materiali o come solidi perfetti.
Questo non vuol dire che la meccanica non entri nello studio
della struttura interna dei corpi. Anzi, è proprio con le leggi della
meccanica (classica e quantistica) che si sono esplorate le proprietà interne
dei corpi. Quello che si vuol dire qui, piuttosto, è che le leggi della
meccanica, per un dato insieme di corpi, riguardano il moto reciproco di quei
corpi e non la loro struttura interna. Lo studio della struttura interna,
dunque, richiede la suddivisione di un corpo nelle parti (mobili) che lo
compongono e l'applicazione delle leggi della meccanica a queste ultime.
Questa procedura s'interrompe quando le leggi della meccanica diventano
inadeguate (non compatibili con le osservazioni). Lo stesso vale per l'
applicabilità su scale mano a mano più grandi (galassie, ammassi di galassie,
ecc.).
 |
 |
|
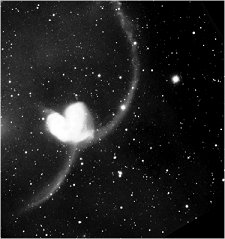
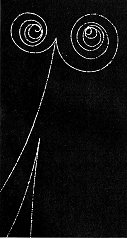
Macroscopico e microscopico: può una
stessa teoria fisica descrivere la collisione di galassie (a sinistra) e
la collisione di particelle elementari (a destra)?
|
Definizione di punto materiale: un punto materiale è un
corpo le cui dimensioni spaziali non hanno alcuna rilevanza ai fini del suo
movimento. Un sistema meccanico può essere costituito da un insieme di punti
materiali.
La sostituzione di un sistema fisico reale (un corpo) con un
ente matematico (punto materiale o insieme di punti materiali) è necessaria
per avviare una formulazione di tipo matematico. L'utilizzo del linguaggio
matematico per esprimere contenuti fisici è un aspetto irrinunciabile e
qualificante della scienza fisica. Attenzione però a non confondere il
linguaggio matematico con il contenuto fisico. A differenza del linguaggio,
che obbedisce a certe regole logiche e formali tali da garantirne l'efficacia
e la consistenza interna, il contenuto fisico di una teoria è soggetto ad un
procedimento di verifica (vero/falso) basato sulle osservazioni empiriche
(misure). Ad ogni grandezza fisica sarà associata una procedura operativa di
misura. Nell'osservazione dei fenomeni saranno stabilite le regole (operative)
per la verifica di una legge entro i margini di indeterminazione delle misure.
Dato che le misure non possono essere infinitamente precise, la validità di
una teoria s'intende verificata, sempre e comunque, entro un margine di
indeterminazione.
La sensatezza e la correttezza della sostituzione di corpi
fisici con punti materiali va giudicata sulla base dell'accuratezza del
risultato atteso. Se per la descrizione di un certo fenomeno è ritenuta
sufficiente una data accuratezza, e se gli effetti dovuti all'estensione
spaziale del corpo fisico (la sua struttura geometrica, la sua composizione,
ecc.) sono trascurabili entro tale accuratezza, allora il corpo fisico può
essere trattato come un punto materiale, con tutti i vantaggi che ne seguono
dal punto di vista della trattazione matematico-formale. Ad esempio, dal punto
di vista dell'attrazione di gravità dovuta alla terra, tolti gli effetti
dell'attrito con l'aria, una patata o una palla da tennis si comportano
esattamente allo stesso modo, ovvero come punti materiali. Con ciò s'intende
che non esistono strumenti sufficientemente precisi per misurare gli effetti
della diversa forma dei due oggetti relativamente all'attrazione verso la
terra; oppure che, se anche questi strumenti esistessero, le differenze
sarebbero talmente piccole da non avere alcun interesse nell'ambito delle
attività usuali associate alle patate e alle palle da tennis. In tale ambito
la teoria che li considera come punti materiali rimarrebbe una buona teoria,
almeno per quanto riguarda l'effetto della gravità. Il punto materiale può
essere visto come l'elemento concettuale sufficiente a rappresentare il moto
di un corpo in certe condizioni ed entro una certa precisione. Il suo utilizzo
è efficace, in quanto si presta ad una trasposizione diretta di osservazioni
empiriche in un linguaggio matematico semplice, ed è anche utile, in quanto
permette di rappresentare in modo unitario il moto di un'ampia classe di
oggetti fisici. Non esiste, invece, una teoria o una legge fisica per il moto
di una specifica patata. Non sarebbe sufficientemente generale, né utile, da
meritare lo sforzo di elaborarla.
Definizione di solido perfetto: un solido perfetto è un
corpo tale che la distanza tra due suoi componenti qualsiasi resti costante nel
tempo.
Vale quanto detto al punto precedente. Il corpo solido
perfetto non esiste in senso stretto. Si tratta di una rappresentazione
astratta di un comportamento riscontrabile, entro una certa precisione, in una
vasta classe di oggetti fisici. Come idealizzazione di tali oggetti, si presta
ad essere utilizzata nel linguaggio delle teorie fisiche in modo efficace ed
utile.
Suddivisione della meccanica: la meccanica comprende la
statica (studio delle condizioni per l'equilibrio meccanico), la cinematica
(studio del movimento indipendentemente dalle cause che lo producono) e dinamica
(studio del movimento come effetto dell'interazione tra i corpi).
Per quanto si tratti di una suddivisione naturale, che
risponde ad esigenze pratiche, essa viene spesso abusata, specie nella
didattica. In realtà, nessuno dei tre settori vive di vita propria. L'eccesso
di schematismo può penalizzare una visione globale dei problemi.
È sintomatico che, dopo aver distinto statica e dinamica,
questo stesso manuale non accenna più esplicitamente alla statica. In effetti,
le leggi della statica possono essere viste come caso particolare di quelle
della dinamica; basta imporre che i punti di un sistema meccanico non si
muovano, per ottenere le condizioni di equilibrio. La trattazione separata
della statica può quindi essere considerata ridondante, se lo scopo è quello
di presentare i fondamenti della meccanica in forma "economica". Tuttavia, non
può essere dimenticato il fatto che statica e dinamica si sono sviluppate
indipendentemente nella storia e che i concetti introdotti nell'uno e
nell'altro campo, pur convergendo verso un unico schema formale, hanno avuto
valenza diversa e hanno contribuito autonomamente all'elaborazione della
teoria generale. Si pensi, ad esempio, al fatto che alcuni pensatori antichi,
come Archimede per citarne uno, erano riusciti a formulare delle leggi
statiche sostanzialmente corrette, come per il funzionamento delle leve o il
galleggiamento dei corpi in acqua, ma non leggi dinamiche altrettanto
efficaci. Questo è avvenuto, non per una presunta propedeuticità della statica
rispetto alla dinamica, quanto per la difficoltà di includere sensatamente il
concetto di tempo in una formulazione quantitativa delle leggi che regolano il
mondo. La statica non richiede un concetto operativo di tempo, la dinamica sì.
"L'inclusione della variabile tempo nelle formule matematiche che esprimono le
leggi fisiche e la scoperta che tale variabile poteva perfino essere elevata
al quadrato nella caduta dei gravi segna un punto cruciale nella cosiddetta
rivoluzione scientifica. A noi oggi può apparire cosa scontata e quasi banale;
ma non lo fu certamente allora. E quanto sarebbe bene far riflettere i giovani
scolari su queste cose, anziché metterle semplicemente sullo stesso piano di
qualunque risultato di osservazione!" (da, Toraldo di Francia, Tempo,
Cambiamento, Invarianza). Naturalmente, una volta incluso propriamente il
tempo, la statica può essere effettivamente concepita come una soluzione
particolare della dinamica, ma non al punto da perdere traccia dell'origine
dei concetti che stanno alla base di entrambe.
Se la statica e la dinamica sono strettamente connesse, la
cinematica appare spesso come un qualcosa di ben distinto; una specie di
cassetto degli attrezzi, in cui si trovano le definizioni utili a descrivere
oggetti che si muovono nello spazio, le equazioni per alcuni tipi particolari
di moto, e così via. Tuttavia, bisogna fare nuovamente attenzione al fatto che
la cinematica non viene "prima" della dinamica, non contiene definizioni e
leggi matematiche che possano vivere indipendentemente dalla dinamica.
Piuttosto, essa contiene in partenza una visione dello spazio, del tempo e del
movimento propria della teoria generale, inclusa la dinamica. Tant'è, ad
esempio, che la caduta della dinamica newtoniana di fronte al problema
dell'invarianza della velocità della luce e la sua sostituzione con le leggi
della relatività ristretta hanno coinciso con la contemporanea riscrittura
della cinematica per intero.
Una trattazione della cinematica troppo distinta dalla
dinamica è fuorviante non solo perché porta a pensare che i suoi concetti
siano "preliminari" alla formulazione di una qualsiasi dinamica (cosa non
vera, come appena discusso), ma anche perché tende a fornire un'immagine della
fisica troppo matematica, in senso semplicistico. Questo accade quando si
confonde il significato matematico di una legge, come s=vt, con il suo
significato fisico. Il moto uniforme, il moto accelerato, il moto circolare,
diventano allora delle astrazioni, distanti dal mondo reale, come semplici
esercizi di algebra e geometria. Per riconoscere il significato fisico, oltre
alla necessaria nozione di misura (e il corrispondente problema della sua
indeterminazione), è pure indispensabile avere una sufficiente nozione fisica
degli ingredienti di ogni equazione (spazio, tempo, velocità, accelerazione,
ecc.). Troppo spesso però, per il timore ingiustificato di mescolare
cinematica e dinamica, si sorvola su tali concetti fornendo, in alternativa,
uno schema assiomatico astratto. Dal punto di vista didattico, una simile
impostazione ha come risultato frequente il fatto che lo studente non coglie
da subito il significato della scienza fisica, i suoi obiettivi e la sua
metodologia; il suo impatto con la fisica sarà piuttosto limitato ad un
complicato esercizio accademico di scarso interesse.
Definizione di sistema di riferimento: un sistema di
riferimento è un corpo solido perfetto, reale o astratto, rispetto al quale si
studia il moto degli altri corpi. Al sistema di riferimento è associato un
sistema di coordinate spaziali più un orologio. Il moto del corpo sarà allora
descritto da variazioni delle coordinate nel tempo. In linguaggio matematico:
q1=q1(t), q2=q2(t), ecc., se
q1, q2, ... sono le coordinate spaziali e t
è il tempo. La traiettoria seguita dal punto nel suo movimento è fissata da
un'equazione del tipo f(q1,q2,...)=0, che si trova
eliminando il tempo t dalle equazioni q1=q1(t),
q2=q2(t), ecc. . I valori delle coordinate e, quindi,
la forma della traiettoria dipendono dalla scelta del sistema di riferimento.
Una scelta ragionevole per studiare il moto nell'usuale spazio a 3 dimensioni è
la terna di coordinate ortogonali cartesiane x,y,z, in modo che la
posizione di un generico punto materiale è fissata dal vettore r =
(x,y,z), che è funzione del tempo, r = r(t). In
alcuni casi può essere più conveniente la scelta di un sistema di coordinate
sferiche o cilindriche. Se il sistema meccanico è vincolato ad un sottospazio
(moto in un piano, o su una superficie curva assegnata, ecc.) s'introducono
delle coordinate ad hoc, dette coordinate generalizzate, che rappresentano i
gradi di libertà effettivi del sistema stesso.
Con queste definizioni si compie il primo passaggio da
concetti intuitivi a concetti operativi, tipico della fisica. Piuttosto che
seguire un'impostazione filosofica riguardo al problema di quale sia l'ultima
essenza dello spazio e del tempo, il fisico si pone da subito il problema di
come lo spazio e il tempo possano essere misurati. Nella definizione di
sistema di riferimento è implicita una qualche procedura per la determinazione
di campioni di misura di lunghezze e tempi, cioè si dà per nota l' esistenza
di oggetti la cui lunghezza è costante e di orologi, basati sulla ripetizione
periodica di certi processi.
Il sistema di coordinate rappresenta allora il metodo più
efficace di esprimere il "dove" e il "quando" di ogni evento fisico, usando il
linguaggio matematico. Per questa sostituzione della realtà fisica con
un'entità matematica vale ancora quanto già detto sulla questione
dell'indeterminazione implicita in ogni misura. Vale la pena inoltre
sottolineare il fatto che l'introduzione di procedure operative per la misura
di spazio, tempo e di tutte le altre grandezze fisiche consente il passaggio
da una percezione "soggettiva" della realtà ad una visione "intersoggettiva".
La percezione soggettiva costituisce il primo canale attraverso cui le
informazioni sul mondo esterno entrano nella coscienza di ciascun osservatore,
attraverso i propri sensi (vista, udito, tatto, ecc.). Il modo di elaborare
tale informazioni da parte del cervello è sicuramente unico per ogni
osservatore. Il tempo può scorrere velocemente o lentamente, le distanze
possono essere lunghe o corte, e così via, a seconda di chi osserva e anche a
seconda del suo "stato d'animo".
Sulle basi della sola percezione soggettiva non si può
sviluppare alcuna scienza fisica, in quanto mancano i presupposti per la
comunicazione di informazioni "quantitative" tra più osservatori. La visione
intersoggettiva si realizza fornendo delle regole per lo scambio di
informazione tra gli osservatori. Una prima regola operativa è quella di far
corrispondere ad ogni elemento di un processo fisico un numero e di usare la
matematica per stabilire relazioni utili tra i numeri che entrano in una certa
classe di processi. In questo modo nascono le "grandezze fisiche" come
elementi propri del linguaggio scientifico. Alle grandezze fisiche si dà una
definizione operativa, indipendentemente dalle valutazioni filosofiche che
possono essere più o meno rilevanti, più o meno assodate. La definizione
operativa di tempo, ad esempio, presuppone l'esistenza di eventi periodici a
cui si assegna a priori un periodo costante. Eventi del genere costituiscono
gli orologi e, in un certo senso, il tempo fisico si identifica con la sua
misura tramite gli orologi. Una simile procedura permette lo scambio di
informazioni intersoggettivo. Se avete dimenticato una libro su una sedia di
un'aula e un vostro amico si presta ad andare a recuperarlo, gli direte, ad
esempio: il libro si trova su una delle sedie della decima fila a partire
dalla cattedra e, precisamente, sulla terza sedia contando da destra. Ogni
persona che entra potrà verificare la veridicità di tale affermazione. Se sul
muro della stanza c'è un orologio funzionante, ciascuno potrà anche dire in
quale istante di tempo esegue la verifica. Tutto ciò corrisponde ad una realtà
fisica intersoggettiva, che parte da percezioni soggettive ma che ne diventa
indipendente (poco importa che uno degli osservatori dica "oggi il tempo non
mi passa più" e un altro sia astigmatico e veda la stanza un po' distorta,
ecc.).
Se il nostro scopo fosse quello di conoscere la realtà in
senso lato, rispondendo a domande del tipo cos'è il tempo, cos'è lo spazio,
ecc., questa concezione operativa delle grandezze fisiche apparirebbe molto
restrittiva ed insoddisfacente. Resta il fatto che la visione operativa, pur
non esaurendo affatto la nostra ambizione di capire il mondo in cui viviamo,
ha portato a dei progressi sostanziali.
C'è un altro aspetto interessante legato all'idea di sistema
di riferimento e alla nozione di spazio. Si pensi al problema di misurare la
distanza tra due oggetti. Se tali oggetti sono relativamente piccoli rispetto
alle dimensioni del nostro campione di lunghezza e sono anche prossimi a chi
fa la misura, allora la lunghezza può essere misurata per confronto diretto
con il campione (il metro del muratore per misurare un muro, ecc.). In molti
casi, invece, la misura è necessariamente indiretta. Si pensi, per esempio, di
misurare la distanza tra i due componenti di una stella doppia. Guardare le
due stelle e localizzarle nello spazio, in questo caso, implica un'assunzione
su come si propaga la luce. Bene, possiamo assumere che lo spazio sia euclideo
e che la luce si propaghi in linea retta. Queste assunzioni, che ci permettono
di eseguire la misura e di verificare le leggi della meccanica per l'orbita
delle due stelle, risultano convenienti nella formulazione della meccanica
classica. Si noti, tuttavia, che il fatto di assumere uno spazio euclideo non
corrisponde ad una legge fisica, ma solo ad una scelta conveniente della
geometria da usare per la rappresentazione dello spazio fisico. Teorie più
elaborate possono implicare scelte diverse, come nel caso della relatività
generale, in cui si assume una geometria non euclidea, con la luce che si
propaga lungo geodetiche, seguendo la curvatura dello spazio-tempo.
 |
 |
|
La distanza tra Plutone e il suo
satellite Caronte (foto a sinistra) può essere misurata usando la
geometria euclidea e l'ipotesi che la luce si propaghi in linea retta.
Lo stesso non si può dire per l'immagine a destra, dove si vede
l'effetto di una "lente gravitazionale": la luce che arriva dalle
galassie piú lontane viene deviata da un campo gravitazionale intenso e
le galassie stesse appaiono deformate, duplicate e spostate rispetto
alla loro posizione reale. Per interpretare l'immagine, in questo caso,
conviene utilizzare uno spazio-tempo curvo e la geometria non
euclidea. |
Definizione di velocità (istantanea): la velocità di un
punto materiale è data dal rapporto
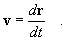
è un vettore orientato secondo la tangente alla traiettoria. Il
modulo è la derivata dello spazio percorso lungo la traiettoria stessa,
v=ds/dt.
Per il moto su un piano può essere utile scomporre la velocità
in una parte radiale e una parte angolare, utilizzando coordinate polari.
La definizione di velocità come derivata dello spazio
percorso rispetto al tempo non è un concetto intuitivo. Se si chiede cos'è la
velocità ad una persona digiuna di nozioni fisiche, vi fornirà probabilmente
una definizione ragionevole basata sull'idea del muoversi in fretta o muoversi
piano, superare o essere superati. Perfino un bambino in età pre-scolare ha
un'idea ragionevole di cosa sia la velocità, ben prima di aver imparato ad
usare un orologio o di aver acquisito il concetto di rapporto tra numeri.
Si può pensare, in effetti, alla velocità come a una
grandezza primaria e si può immaginare una procedura operativa per definire un
campione di misura basato su oggetti che si superano. La cosa non è
impossibile e risponderebbe meglio al concetto intuitivo di velocità. Tuttavia
il risultato sarebbe scarsamente utile dal punto di vista pratico (dovremmo
mettere dei carrelli mobili su dei binari paralleli, con configurazioni
complicate,...). è quindi una ragione di praticità che ci porta a definire la
velocità come rapporto di spazi e tempi. Si noti che questo, tuttavia,
comporta alcune difficoltà. La prima riguarda la formulazione storica della
teoria: il calcolo infinitesimale, e quindi il concetto di derivata, non
esisteva prima di Newton. Questo ha implicato un lavoro in più per Newton e
per i suoi contemporanei, come Leibniz, che hanno dovuto inventarsi il calcolo
infinitesimale proprio per sviluppare la meccanica. La seconda difficoltà
riguarda la didattica, dato che gli studenti che affrontano per la prima volta
la fisica non possiedono ancora, di solito, le nozioni elementari del calcolo
delle derivate. Questo implica che la definizione di velocità, una delle prime
da fornire allo studente, manca del suo supporto matematico naturale e deve
essere sostituita con un procedimento di limite "empirico" a partire dalla
velocità media. Di nuovo, questo produce nello studente la sensazione che la
fisica sia un esercizio astratto e complicato piuttosto che uno strumento
efficace di indagine della realtà.
Definizione di velocità media: grandezza pari al rapporto
tra spazio percorso e intervallo di tempo corrispondente
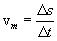
Nel limite in cui l'intervallo di tempo diventa infinitesimo,
la velocità media coincide con la velocità istantanea.
Spesso la velocità viene prima introdotta come velocità
media, passando successivamente al caso di intervalli di tempo sempre più
piccoli, fino a coincidere con la velocità istantanea. Si fa anche distinzione
tra il concetto puramente matematico di velocità istantanea (come derivata) e
quello fisico di rapporto di intervalli piccoli ma non nulli. Il passaggio al
limite non è infatti realizzabile, in senso stretto, per grandezze fisiche
soggette, comunque, all'indeterminazione della misura. La distinzione tuttavia
è puramente convenzionale, come è convenzionale la definizione stessa di
velocità. Supponiamo ad esempio di aver definito la velocità come grandezza
"primaria", usando opportuni campioni di misura basati su carrelli mobili. Lo
strumento che misura la velocità in questo modo sia chiamato, ad esempio,
"tachimetro a carrelli". Poi, immaginiamo un esperimento in cui si muovano
degli oggetti su un piano orizzontale, facendo in modo che la loro velocità,
misurata con il "tachimetro a carrelli" risulti costante. Successivamente, si
metta da parte il tachimetro e si eseguano gli stessi identici movimenti
misurando, con aste e orologi, le lunghezze percorse e i tempi impiegati a
percorrerle. In questo modo otterremmo, entro l'indeterminazione sperimentale
degli strumenti, la seguente legge fisica: un corpo che si muove per un tempo
t a velocità costante v percorre uno spazio s dato da s=kvt, dove k è una
costante che dipende dalle unità di misura scelte. Tuttavia, la definizione
operativa di velocità, come grandezza primaria, implica difficoltà pratiche e
una scarsa precisione di misura. Allora può risultare preferibile usare la
legge s=kvt per ridefinire la velocità stessa. Basta intendere l'uguaglianza
in senso strettamente matematico, togliendole ogni riferimento
all'indeterminazione della misura e assumendo la costante k uguale a 1. In tal
modo la nuova definizione di velocità sarà v=s/t. La legge del moto uniforme
avrebbe perso la sua valenza di legge fisica; in cambio, avremmo ottenuto una
definizione operativa di velocità più efficace e precisa. Non vi è nulla di
criticabile in questa scelta, purché si distingua, ad ogni passo, il
significato fisico e matematico delle varie operazioni compiute. Vista in
questo modo, la velocità media ha una definizione non meno "matematica" di
quella istantanea.
Ad un livello più elementare, la distinzione tra velocità
istantanea e media può portare ad altre ambiguità. Ad esempio, in un testo di
fisica per le scuole superiori di recente pubblicazione, dopo aver definito la
velocità media come v=s/t, si trova la seguente affermazione: "per la velocità
istantanea vale la stessa definizione, purché si prendano intervalli di tempo
abbastanza piccoli da poter considerare costante la velocità al loro interno".
Evidentemente una tale definizione è circolare. Non è infatti possibile, a
rigor di logica, stabilire se la velocità sia costante, prima ancora di averla
definita compiutamente. Si può pensare che quel testo (tra l'altro il libro si
intitola "Manuale di Fisica") sottintenda un ragionamento più complesso di
questo tipo: una volta definita la velocità media, si supponga di compiere la
misura su intervalli di tempo piccoli, scelti a piacere intorno ad un instante
t assegnato. Se il risultato non dipende dalla lunghezza di tali intervalli,
compatibilmente con l'indeterminazione delle misure, né dalla scelta degli
estremi, purché comprendano l'istante t, allora si dice che la velocità è
costante negli intervalli considerati e il suo valore coincide con la velocità
istantanea in t. Una procedura del genere, o qualche altra ad essa
equivalente, sarebbe complicata da spiegare agli studenti. Non per questo,
però, è corretto sostituirla con un'evidente tautologia, come quella del
Manuale di Fisica menzionato sopra.
Sempre riguardo alla distinzione tra velocità media e
velocità istantanea, vale la pena soffermarsi su un aspetto storico
interessante (T.S. Kuhn, La struttura delle rivoluzioni scientifiche).
Prendiamo il caso di un sasso che cade. Aristotele ha sicuramente potuto
osservare la caduta libera di un sasso o di altri oggetti, e così pure i suoi
discepoli nei secoli successivi. Anche Galileo (1564-1642) ha potuto osservare
lo stesso fenomeno. Risulta che Galileo sia riuscito a descriverne il moto
correttamente (moto con accelerazione costante, velocità che cresce
proporzionalmente al tempo, spazio che cresce col quadrato del tempo), mentre
gli aristotelici non vi erano riusciti. In un certo senso, è possibile
ricondurre questo successo (e insuccesso) ad un cambiamento di parametri
ritenuti pertinenti alla descrizione del fenomeno. Guardando un sasso che
cade, Aristotele ne deduceva un cambiamento di stato (il sasso sta lontano dal
suo luogo naturale e successivamente lo raggiunge) piuttosto che un processo
continuo. Il sasso, comunque mosso all'inizio, era costretto a raggiungere per
sua natura il suo stato finale di riposo. Ciò che interessa è, dunque, la
distanza "che lo separa dal punto finale", piuttosto che la distanza "a
partire dal punto iniziale". Ne consegue che le misure rilevanti per
caratterizzare il movimento erano la distanza totale percorsa e il tempo
totale trascorso, parametri che forniscono quella che noi chiamiamo velocità
media. La cultura tardo medioevale, invece, modifica il modo di osservare il
movimento, introducendo l'idea di "impetus" (ad esempio con Guglielmo da
Occam, c.1290-1349, e Buridano, c.1295-1366). Il sasso, a seconda di com'è
mosso all'inizio, possiede un certo "impetus" che gli è stato fornito dalla
spinta iniziale. Questo impetus può variare durante il moto per effetto della
resistenza dell'aria, o per il concomitante effetto del moto naturale verso il
basso. Per caratterizzare il moto, in tal caso, è necessario seguirne
l'andamento nel tempo e la distanza "a partire da" diviene ben più importante
della distanza "che separa da". Ciò conduce in modo naturale alla nozione di
velocità istantanea. è su queste basi che Galileo può estrarre dalle
osservazioni le leggi dell'isocronismo dei pendoli e del moto di caduta sui
piani inclinati. Come dire che, per arrivare ad una buona teoria, non è
sufficiente l' osservazione passiva dei fenomeni, ma serve un criterio "a
priori" per scegliere i parametri efficaci a tradurre l'osservazione in una
conoscenza compiuta.
Definizione di accelerazione: l'accelerazione, che
caratterizza le variazioni di velocità nel tempo, è data dal rapporto
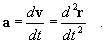
Di nuovo, nel caso, di un moto in un piano, può essere
conveniente introdurre un'accelerazione radiale e un'accelerazione angolare.
Oppure, lungo la traiettoria si possono individuare le accelerazioni normale e
tangenziale (perpendicolare e parallela, punto per punto, alla traiettoria
stessa).
Definizione di moto uniforme e moto uniformemente
accelerato: si ha moto uniforme quando v=costante. Allora a=0
e s=v(t-t0), se t0 è un istante iniziale arbitrario. Si
ottiene invece moto uniformemente accelerato quando a=costante. Allora
v=v0+a(t-t0), con v0
velocità iniziale al tempo t0, e lo spazio percorso aumenta con il
quadrato del tempo.
Moto di traslazione e moto di rotazione: nel caso dei
solidi perfetti bisogna distinguere, nel movimento complessivo del corpo, un
moto di pura traslazione, in cui tutte le traiettorie delle singole parti del
corpo sono parallele tra loro, e un moto di rotazione, in cui tutte le parti del
corpo compiono un moto circolare attorno ad un certo asse. L'asse di rotazione
può pure variare nel tempo. Il moto di rotazione è caratterizzato dalla velocità
angolare (rapporto di angoli e tempo).
2. Dinamica del moto di traslazione (o dinamica del punto
materiale)
Prima legge di Newton: tutti i punti materiali conservano
il loro stato di riposo o di moto rettilineo uniforme fino a quando l'azione di
altri corpi non li fa uscire da tale stato.
Questa legge è detta principio di inerzia e il moto di un punto
materiale non sottoposto a forze si chiama inerziale. Un sistema di riferimento
in cui vale il principio di inerzia è detto sistema inerziale.
Notiamo prima di tutto che l'azione di altri corpi è
identificata qui con l'effetto di forze. La chiave di lettura del principio di
inerzia, così formulato, è quindi il concetto di forza. Tuttavia, va detto che
il concetto di inerzia esisteva prima di Newton e, quindi, prima del concetto
di forza tale come appare nella meccanica newtoniana. Cartesio (1596-1650)
aveva già formulato un principio di inerzia, basato però su categorie
logico-filosofiche piuttosto che sulle osservazioni ("1. Ciascun corpo tende a
conservare lo stato in cui si trova e mai lo muta se non per cause esterne:
nessun corpo si arresta da se stesso. Il riposo è uno stato contrario al
movimento, e nessuna cosa si dirige per natura verso il suo contrario. Solo la
resistenza degli altri corpi può arrestare il movimento di un oggetto, e non
vi è fluido che non possa diminuire la velocità più dell'aria. 2. Ciascun
corpo tende a conservare il movimento seguendo un moto rettilineo, sebbene sia
costretto per altri motivi a muoversi in diverse direzioni. Dio infatti
conserva la materia nello stato in cui essa si trova in ciascun istante: ora,
in ciascun istante il corpo tende a muoversi rettilinearmente: infatti una
pietra che, legata ad uno spago, ruotasse violentemente intorno alla mano,
partirebbe secondo la direzione della tangente al cerchio descritto"). Anche
Galileo formulò un principio di inerzia ("Imagino un mobile lanciato su un
piano orizzontale e rimosso ogni impedimento: già sappiamo che il moto si
svolgerà equabile e perpetuo sul medesimo piano, qualora questo si estenda
all'infinito"). Il "già sappiamo" di Galileo sottintende l'esecuzione di prove
sperimentali e, per questo, il suo principio è più fisico di quello di
Cartesio. A entrambi tuttavia mancava un chiaro concetto di forza e, in tal
senso, il loro principio di inerzia rimane sostanzialmente cinematico.
Per comprendere, il principio di inerzia è utile ragionare
sulla relatività del moto rispetto alla scelta del sistema di riferimento. Si
può dire: il principio di inerzia vale solo nei sistemi inerziali. Oppure: si
chiamano sistemi inerziali quelli in cui vale il principio di inerzia. Prese
alla lettera, queste affermazioni sono delle tautologie. Il punto di partenza
rimane la verifica sperimentale (che non è per nulla banale e che richiede,
come dice Galileo, la rimozione degli "impedimenti"). Si tratta di trovare dei
sistemi di riferimento nei quali l'enunciato del principio di inerzia sia
valido entro un'indeterminazione sufficientemente piccola. Ad esempio, il
sistema avente il sole come origine e tre stelle lontane come direzione degli
assi cartesiani è uno di questi sistemi, se ci si limita a studiare i moti
locali nel sistema solare. Il principio di relatività stabilirà poi che tutti
i sistemi che si muovono di moto uniforme rispetto a questo sono da
considerare buoni sistemi inerziali, entro la stessa indeterminazione. Va
ricordato, a questo proposito, che la principale motivazione di Galileo nella
ricerca di un principio di inerzia era quella di convincere i suoi
contemporanei sul fatto che la rotazione della terra, prevista da Copernico,
non contraddiceva l'assenza apparente di un moto complessivo della superficie
terrestre, dell'atmosfera e di quant'altro sta sulla terra. In realtà, un
laboratorio fissato alla superficie terrestre non costituisce un sistema
inerziale, dato che il suo moto non è uniforme ma soggetto ad un'accelerazione
centripeta (si pensi al pendolo di Faucault), ma lo è quanto basta per dare
ragione a Galileo nell'ambito delle osservazioni da lui discusse.
La verifica sperimentale del principio d'inerzia, come di
ogni altro principio, è non banale, come già accennato sopra, non solo per
questioni metodologiche, come la rimozione degli "impedimenti" nello spirito
della "sensata esperienza" galileiana, ma anche perché bisogna bene intendersi
sul significato stesso della verifica, non riducibile ad un singolo
esperimento di validazione o falsificazione. Nel caso del principio d'inerzia
(o, equivalentemente, dell'inerzialità di un sistema di riferimento) la
verifica non può essere ricondotta ad un esperimento in cui si misuri la
velocità di un oggetto sottoposto a forze con risultante nulla. Ciò
produrrebbe un circolo vizioso. Infatti, l'unico modo che avremmo per
affermare che la risultante delle forze è nulla sarebbe quello di osservare il
moto uniforme!
Per uscire da questa ambiguità dobbiamo affermare che il
principio di inerzia, come gli altri princìpi della dinamica, non è una
descrizione diretta di fatti sperimentali, ma è un'ipotesi che costituisce un
punto di partenza per la descrizione del moto. La verifica della validità dei
princìpi avviene solo sulla base di una "compatibilità complessiva" tra le
diverse osservazioni e le diverse leggi derivate dai princìpi stessi. Ogni
ipotesi di partenza è associata ad un nuova intuizione su come le cose debbano
comportarsi. Nel caso del principio di inerzia, l'idea è quella di assegnare
alla materia una nuova proprietà fondamentale, l'inerzia appunto, che ne
caratterizza la tendenza a mantenere il suo stato di quiete o di moto
uniforme. Per definire lo stato di quiete o di moto è necessario stabilire
anche un principio di relatività che garantisca al significato di inerzia una
invarianza rispetto ai sistemi di riferimento. Fatto questo, lo stato di
quiete e quello di moto uniforme sono del tutto equivalenti (la quiete
assoluta non esiste più) e si apre la porta alla comprensione dei moti diversi
da quello uniforme.
Prendendo spunto da queste ultime considerazioni, possiamo
soffermarci sul significato dei termini "principio" e "legge", che spesso sono
considerati intercambiabili (in questo manuale, in particolare, la
distinzione, se c'è, non viene mai giustificata). Ciò ha a che fare con i
fondamenti del metodo scientifico ed è impossibile farne qui una trattazione
soddisfacente. Di nuovo, il problema risiede essenzialmente nella procedura di
validazione attraverso il confronto con le osservazioni. Come già detto sopra,
nell'ambito di una teoria generica si tende a svincolare alcune leggi dal
confronto con le osservazioni dandogli valenza di principio: si intende con
questo dire che l' enunciato di un principio si trasforma di fatto nella
definizione di un concetto fisico e, in quanto definizione, non richiede la
verifica sperimentale. Questa affermazione non va fraintesa: anche i princìpi
devono essere compatibili con le osservazioni, ma la loro validità dipende da
una valutazione globale su tutte le leggi fisiche che seguono dai princìpi di
partenza. Le singole leggi sono materia di verifica sperimentale, soggetta
all'indeterminazione delle misure. Se un insieme di leggi fisiche dedotte da
un insieme ristretto di princìpi è compatibile con tutte le osservazioni (nel
senso che non si sono ancora trovate osservazioni che lo confutino), allora si
dirà che i princìpi erano validi e che l'unione di quei princìpi e di quelle
leggi costituisce una buona teoria fisica.
Il fatto di distinguere leggi e princìpi è sostanzialmente
una procedura di comodo, adatta a formulare la teoria secondo uno schema
deduttivo assiomatizzato. In quanto tale, la suddivisione di princìpi e leggi
è piuttosto arbitraria e riflette una concezione del mondo fisico che si
modifica a seconda delle epoche e delle scuole di pensiero. A questo proposito
ci sono almeno due osservazioni che meritano di essere fatte. La prima è che,
sulla base del grado di arbitrarietà insito in questa procedura, si potrebbe
essere tentati di dare eccessiva enfasi al carattere convenzionale di una
teoria, arrivando a dire che le teorie fisiche "non sono altro che" insiemi
coerenti di definizioni (princìpi) arbitrarie. Una tale idea è stata sostenuta
da vari filosofi-epistemologhi in passato, specie in connessione con lo
strumentalismo, secondo il quale una teoria fisica "non è altro che" uno
strumento utile a collegare tra loro fatti osservati e prevederne di nuovi.
Anche se lo strumentalismo gode ancora di un certo favore tra i fisici (magari
non in forma consapevole e non come teoria epistemologica codificata), non
credo che gli stessi accetterebbero le tesi estreme del convenzionalismo (o
del "nominalismo"). E perfino un eminente fisico-matematico come Poincaré, che
pure era ritenuto un convenzionalista, non poteva fare a meno di criticare le
tesi dei nominalisti, essendo consapevole che una teoria fatta di soli
princìpi non è una teoria fisica ma un'insieme coerente di definizioni (nomi)
e che, al contrario, le teorie elaborate dai fisici hanno un contenuto
empirico non riconducibile ad un insieme di definizioni.
La seconda osservazione è che il bisogno di formulare le
teorie fisiche secondo schemi deduttivi assiomatizzati non va confuso con lo
scopo delle teorie stesse. Lo scopo del fisico non è quello di arrivare a
formulare una teoria assiomatizzata, ma di proporre congetture innovative da
sottoporre alla verifica sperimentale; a priori non è necessario che tali
congetture, per trasformarsi in una buona teoria, si presentino nella forma di
uno schema deduttivo. Il fatto che una teoria presentata in forma deduttiva
(pochi principi seguiti da implicazioni logiche-matematiche rigorose) ci
sembri migliore è legato alla maggior controllabilità della teoria, cioè alla
possibilità di seguire nel dettaglio tutte le sue implicazioni (che la rendono
ricca di contenuti) e di controllarne la validità passo per passo. Tradotto in
un esempio "meccanico", tutto ciò è paragonabile al motore di un'automobile:
ci si aspetta che sia strutturato per bene, con tutti gli elementi
fondamentali in evidenza e tutte le connessioni ben disposte, in modo che un
meccanico riesca ad individuare rapidamente un eventuale difetto, grave e
insignificante che sia. Ciò non toglie che un motore possa funzionare
egualmente bene, anche con cavi e tubi sparpagliati in apparente disordine.
Concetto di forza: la forza è una grandezza vettoriale che
misura l'azione meccanica esercitata su un punto materiale e su un corpo da un
altro corpo o campo.
Il concetto di campo introduce qui una circolarità nella
definizione. Infatti, se il campo qui è inteso come campo di forze, ma allora
non si capisce come la forza possa misurare l'azione meccanica esercitata
dalle forze. è evidente che il concetto di campo è stato aggiunto per
suggerire l' esistenza di azioni meccaniche prodotte da qualcosa di diverso da
altri corpi. Ma questo implica una visione moderna della fisica, assai
posteriore alla formulazione della meccanica. In questo senso, l' aggiunta del
termine "campo" in questo punto del manuale appare una forzatura non
necessaria.
Dal principio di inerzia segue che l'interazione mutua tra i
corpi è la causa della variazione del loro stato di moto. Tale interazione
provoca, inoltre, la deformazione dei corpi. La misura della deformazione di uno
stesso corpo elastico permette di confrontare le forze tra loro e stabilire
campioni di misura.
Questa definizione di forza è priva di significato se presa
separatamente dalla II legge di Newton. Il principio d' inerzia, infatti, non
è sufficiente a introdurre "operativamente" le forze a partire solamente dalla
sua violazione. Inoltre il concetto di deformazione, introdotto quasi in
alternativa all'idea di variazione dello stato di moto, appare come un corpo
estraneo nell' ambito dei fondamenti della meccanica e non può nemmeno essere
assunto come noto a priori. La stessa legge di Hooke, che descrive il
comportamento dei corpi elastici in regime lineare, può essere applicata
operativamente alla misura delle forze solo dopo aver dato senso compiuto ai
concetti di forza, peso e massa. è ben vero, infatti, che il confronto tra le
forze per mezzo di un insieme di molle uguali, disposte in serie o in
parallelo, può costituire una procedura per definire le forze
indipendentemente dalle leggi della dinamica; ma nessuno ci garantisce
sull'applicabilità della legge di Hooke (deformazioni proporzionali alla forza
applicata) alle molle usate come campione. In altri termini, la preparazione
di un dinamometro, sufficientemente preciso per verificare le leggi della
dinamica, richiede un' idea chiara dei concetti di forza, massa e peso.
Tutto questo ha anche a che vedere con il giudizio soggettivo
sull'efficacia delle definizioni. Come già discusso nel caso della velocità,
infatti, usare una legge fisica piuttosto che un'altra per definire una
grandezza è un fatto in certa misura convenzionale; l' importante è saper
riconoscere, all'interno di una teoria, o di una delle sue possibili
formulazioni alternative, ciò che è definizione da ciò che è legge,
quest'ultima essendo vincolata alla verifica sperimentale. Un insieme di
definizioni sarà tanto più efficace quanto più semplici (nel senso di
facilmente controllabili) ed efficaci (nel senso di ricche di contenuto
empirico) sono le leggi fisiche che da esse derivano.
In conclusione, insistere su una definizione di forza che
preceda la II legge di Newton può essere pericoloso, sia per le circolarità
che possono accompagnare tale definizione sia perché, storicamente, il
concetto operativo di forza e la II legge di Newton hanno avuto origine dalla
stessa idea (il concetto intuitivo di forza è antecedente, ma inefficace ai
fini pratici della fisica). Analogo ragionamento si applica al concetto di
massa.
Va detto, per inciso, che la fisica moderna non assegna più
alla forza quel ruolo preminente che aveva nelle prime formulazioni della
meccanica. Al suo posto, come grandezza fondamentale, si mette normalmente
l'energia, mentre le forze vengono ridotte a grandezze di comodo, introdotte
artificialmente per ragioni pratiche nel risolvere singoli problemi. Il fatto
che la meccanica si sia sviluppata storicamente attorno al concetto di forza,
e che tuttora questo concetto sia importante nell'insegnamento della fisica, è
conseguenza della nostra visione antropomorfa della realtà. Appare naturale,
infatti, associare il movimento di un oggetto qualsiasi ad uno sforzo
muscolare che, tradotto in termini quantitativi, porta all'idea di forza.
Anche dell'energia si può avere una visione intuitiva basata sulla "fatica"
fatta (o sprecata) in un certo processo. Ma l'uomo, inteso come oggetto
"muscolare-sensoriale-meccanico", non è un buon misuratore di energia, nel
senso che risulta più semplice quantificare la forza muscolare esercitata per
spostare un oggetto piuttosto che l'energia impiegata (si pensi, ad esempio,
al fatto che i nostri muscoli fanno fatica anche quando trasportano un peso
orizzontalmente, mentre questo non implica alcuna variazione di energia
potenziale).
A questo proposito vale la pena sottolineare che questo
passaggio da grandezze "antropomorfe", più legate ai sensi e alle percezioni
soggettive, a grandezze in cui il carattere antropomorfo diventa via via
minore non è una anomalia di pochi concetti e poche teorie ma, al contrario, è
una delle caratteristiche peculiari del progresso scientifico. E' un dato di
fatto che le teorie fisiche più recenti (relatività e meccanica quantistica)
sono formulate usando grandezze alquanto astratte (tensore energia-momento,
funzioni d'onda, tanto per citare esempi). Sembra addirittura che sia proprio
l'introduzione, di volta in volta, di grandezze nuove, completamente (e
arditamente) svincolate dalla sensorialità, a permettere la formulazione di
teorie più generali e complete. Non occorre scomodare le funzioni d'onda della
meccanica quantistica per averne un esempio significativo; basta pensare a
quel passaggio chiave della fisica dell'800 che è stato l'introduzione del
concetto di entropia. Questa grandezza, che ha ben poca attinenza con le
percezioni dirette dell'uomo, ha permesso di dare un'interpretazione profonda,
microscopica, del secondo principio della termodinamica, facendo fare un salto
in avanti alla fisica dopo lo stallo che si era creato nei tentativi di
rendere tale principio compatibile con la reversibilità delle equazioni del
moto newtoniane e con la conservazione dell'energia.
L'idea che le teorie fisiche diventino migliori quando
includono concetti sempre meno antropomorfi è in linea con la visione di una
scienza che tenda ad un linguaggio intersoggettivo, in cui la percezione
individuale perde mano a mano importanza. E' invece in contrasto con la
visione, storicamente ben radicata, di una scienza tutta basata
sull'osservazione diretta dei fatti; questa visione, che viene indicata
normalmente col termine di "osservazionismo", ha avuto origine dal pensiero
filosofico di Bacone ed ha ispirato, in forme diverse, numerose correnti di
pensiero. Un punto debole dell'osservazionismo sta nel considerare i fatti
osservati come sola fonte da cui estrarre i concetti che compongono una
teoria. Di conseguenza, per progredire nella conoscenza, lo scienziato deve
dapprima liberarsi di tutti i possibili pregiudizi (filosofici) e poi, con la
mente pura, rivolgersi alla Natura per dedurne i concetti e le leggi, come si
fa quando si legge un libro. La debolezza di questo punto di vista sta nel
fatto che la mente pura di un osservatore libero da ogni pregiudizio teorico
è, di fatto, una mente vuota, che nessuna osservazione può da sola riempire di
contenuti. Al giorno d'oggi prevale tra i fisici l'opinione che i concetti non
si estraggono direttamente dai fatti osservati, ma costituiscono invece gli
elementi base, teorici, di una possibile interpretazione dei fatti. Nel caso
del concetto di forza, non sono nè le osservazioni astronomiche (riassunte
nelle leggi di Keplero), nè le osservazioni di Galileo sul moto dei gravi ad
imporre da sè un concetto di forza. Quest'ultimo viene introdotto da Newton
come elemento portante di una teoria in grado di fornire un'interpretazione
nuova per quelle stesse osservazioni e, inoltre, altre predizioni per
osservazioni ancora da fare. Lo stesso si potrebbe dire per l'energia,
l'entropia, le funzioni d'onda e ogni altro concetto fisico.
Concetto di massa: la massa di un corpo è una grandezza
fisica che tiene conto delle proprietà di inerzia e di gravitazione del corpo
stesso. La massa è una grandezza scalare per cui valgono le seguenti proprietà:
è additiva (la massa di un corpo scomposto in parti arbitrarie è la somma delle
masse di ciascuna parte), non dipende dalla velocità del corpo e, per un sistema
isolato, si conserva (non dipende la tempo).
La massa che compare nella II legge di Newton caratterizza le
proprietà inerziali e viene detta massa inerziale. La massa che compare nella
legge di attrazione universale caratterizza le proprietà gravitazionali e viene
detta massa gravitazionale. Si verifica che la massa inerziale e la massa
gravitazionale sono uguali. Ciò permette di misurare la massa con semplici
bilance.
Per un corpo esteso si può definire una densità di massa, in
modo che la massa totale sia l'integrale della densità eseguito sul volume
occupato dal corpo stesso. Per un corpo omogeneo la massa totale è il prodotto
della densità per il volume.
Per un sistema di punti materiali si può definire un centro di
massa (o centro di inerzia) dato dal raggio vettore
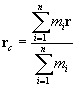 .
.
Come nel caso della forza, questa definizione di massa non
viene "prima" della II legge di Newton ma "assieme" ad essa. Anzi, in questa
versione sono contenute informazioni che vengono "dopo", come l'indipendenza
dalla velocità e la conservazione della massa di un sistema isolato. Le
definizioni di forza e massa sono due esempi di come non si possa scrivere un
"manuale" senza avere prima una visione completa delle conoscenze da trattare;
in altri termini, le nozioni scientifiche non procedono per accumulo in
sequenza!
Sia la forza che la massa mancano, nel manuale, di un
enunciato che risponda a "cos'è la forza?" o "cos'è la massa?", non solo nel
senso, ovvio, che non ci si pone problemi filosofici sulla loro essenza
ultima, ma anche che non vengono fornite definizioni operative autonome
rispetto alla II legge. Esse sono invece introdotte come ingredienti di leggi
fisiche (la legge di Hooke, la II legge di Newton, la legge di gravitazione
universale, ecc.) e, per questo motivo, non appaiono separabili da queste.
Se la forza, come lo spazio e il tempo, ammette una
concezione intuitiva diretta, grazie alla nostra percezione sensoriale
(percezione del movimento del nostro corpo nello spazio e delle resistenze al
moto , tramite le sensazioni muscolari, visive, tattili, ecc.), per la massa
la questione sembra più delicata. Un fisico moderno che si occupa di struttura
della materia vede la massa di un corpo come la somma delle masse delle
particelle elementari che lo costituiscono, i protoni, i neutroni, gli
elettroni. Sa anche che la massa e l'energia sono strettamente legate, per cui
la massa di un aggregato di particelle non è soltanto una somma aritmetica
delle singole masse elementari, ma contiene anche un contributo che viene
dalla cosiddetta energia di legame. In effetti, la continua pubblicazione di
tavole aggiornate, dove vengono riportati i valori della massa e di altre
caratteristiche (carica, spin, ecc.) delle cosiddette particelle elementari,
riflette la tendenza a catalogare gli elementi della realtà (o delle teorie
fisiche) secondo gli schemi teorici correntemente accettati. Questa tendenza
può essere vista come prodotto di un'impostazione filosofica "essenzialista",
ovvero l'idea che lo scienziato debba fornire una descrizione del mondo basata
sulla ricerca dell'"essenza" delle cose, la "natura essenziale" delle cose al
di là delle apparenze. Newton era effettivamente vicino a questa visione, e la
massa da lui introdotta voleva essere proprio un pezzo di questa "essenza" dei
corpi materiali, quello necessario a spiegarne il moto. Una visione opposta è
quella nominalista, dove pure la classificazione delle proprietà delle
particelle è importante ma per motivi diversi: la classificazione rigorosa di
tali proprietà si identifica con la definizione (convenzionale) delle
particelle stesse. Una particella che ha una tal massa, una tal carica e tale
spin, si chiama elettrone. Se si trova una particella che coincide con tutte
le proprietà classificate per l'elettrone tranne una, allora si introdurrà
ad hoc la definizione di una nuova particella, e così via. In questo
senso, la tabella delle proprietà particelle elementari diventa un elenco di
"nomi" e dei loro significati, espressi nel linguaggio proprio (convenzionale)
della fisica. Né questa visione nominalista, né quella essenzialista, possono
essere accettate acriticamente. La prima disconosce ai fisici la capacità di
porre il loro linguaggio (le loro teorie) in relazione con la realtà
extra-linguistica (i fatti sperimentali). La seconda attribuisce agli stessi
fisici un compito improprio, quello di formulare per mezzo delle loro teorie
le "risposte ultime" alle domande sulla natura e sulla realtà in generale.
In ultimo, notiamo che una visione atomistica della materia,
anche se in una forma primitiva e priva di possibili verifiche sperimentali,
era sottintesa nella meccanica newtoniana. Il concetto teorico che sta alla
base della descrizione dei corpi materiali infatti è il punto materiale, o
particella. Quindi la materia è considerata discontinua a priori. Come
vedremo, ciò conduce direttamente all'idea di azione a distanza e ai vari
problemi che quest'idea porta con sé.
Concetto di quantità di moto: la quantità di moto di un
punto materiale è il vettore definito dal prodotto della massa per la
velocità
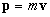 .
.
Nel caso di un sistema di punti materiali basta sommare le
singole quantità di moto dei componenti per ottenere quella totale.
La seconda legge di Newton: la variazione elementare della
quantità di moto di un punto materiale è uguale all'impulso elementare della
forza applicata
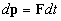 .
.
Oppure
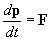 .
.
L'impulso della forza per un intervallo finito di tempo è
l'integrale dell'impulso elementare Fdt nello stesso intervallo di tempo.
Se la massa del corpo è costante, la seconda legge può essere scritta nella
forma
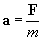 .
.
Ovvero, l'accelerazione di un punto materiale ha la stessa
direzione della forza ad esso applicata, è proporzionale a tale forza e
inversamente proporzionale alla sua massa. L'equazione che dà la relazione tra
l'accelerazione e la forza è anche detta equazione differenziale del moto.
Per la seconda legge di Newton vale un principio di
sovrapposizione: se più forze agiscono simultaneamente su un punto materiale,
ognuna di esse comunicherà una accelerazione che è determinata dalla seconda
legge di Newton, come se le altre forze non esistessero. L'accelerazione totale
è fissata dalla somma (risultante) delle forze.
Salta subito all' occhio il fatto che il principio di inerzia
(o prima legge di Newton) appare come un caso particolare della II legge.
Basta annullare le forze a secondo membro per ottenere accelerazione nulla e,
quindi, velocità costante.
Sembra quindi che la formulazione della meccanica, già nelle
sue poche leggi fondamentali, sia clamorosamente ridondante. è questa anche
una delle maggiori critiche sollevate alla meccanica newtoniana ad esempio da
Mach (E. Mach, La meccanica nel suo sviluppo storico-critico, ed.
Boringhieri). Tuttavia va ricordato che il processo che ha portato al
principio di inerzia è precedente alla formulazione della II legge; esso
contiene un'informazione maggiore di quanta ne risulterebbe trattandolo
semplicemente come caso particolare della II legge. Il principio di inerzia,
infatti, compendia vari aspetti collegati alla comprensione della relatività
del moto, il problema degli "impedimenti" al moto, il ribaltamento della
visione aristotelica del "luogo naturale" a cui tendono i corpi, la
rielaborazione del concetto tardo-medioevale di "impetus" in termini di
quantità misurabili. Tutto ciò risulterebbe nascosto, in parte o del tutto, se
la prima legge venisse declassata a caso particolare della seconda.
Se pure si volesse tralasciare l'aspetto storico, rimane il
fatto che la seconda legge ha senso solo se si precisa il sistema di
riferimento nel quale questa legge è valida. Si può definire tale sistema di
riferimento solo facendo ricorso alla prima legge, la quale afferma
l'esistenza di sistemi di riferimento nei quali un punto materiale libero si
muove di moto uniforme. Senza questo prerequisito, la seconda legge perde
significato e, per questo motivo, non contiene in sé la prima legge.
A tale proposito si può affermare che un atteggiamento
eccessivamente sintetico non è sempre utile. In effetti, è pur vero che tutte
le leggi fisiche possono essere riscritte nella forma A=0 (o in forma di
disequazione A>0), portando al membro di sinistra tutti i termini delle
equazioni associate alle leggi fisiche. L'apparente eleganza formale,
tuttavia, nasconderebbe gran parte delle informazioni utili. Una versione più
nobile di questa tendenza alla sintesi è l'idea che la scienza, per essere
efficace, debba basarsi su criteri di "economicità". Una teoria fisica è
migliore di un'altra se spiega la stessa classe di fenomeni utilizzando il
minor numero di ipotesi di partenza e se le leggi che ne conseguono sono
sufficientemente generali, comode da utilizzare e facili da insegnare. Questa
economicità riguarda non tanto il giudizio sull'oggetto della conoscenza,
quanto l'ordine, la struttura della teoria. Ma la struttura della teoria non è
un fatto secondario; essa può determinare la qualità e la rapidità degli
sviluppi successivi. Si pensi, per citare un caso importante, alle equazioni
di Maxwell che riassunsero in modo elegante ed "economico" le conoscenze
precedenti sull'elettricità e il magnetismo. L'introduzione, da parte di
Maxwell, di un termine aggiuntivo nelle equazioni (la cosiddetta corrente di
spostamento), non in seguito a osservazioni ma sulla base di criteri di
eleganza e simmetria delle equazioni stesse, ha poi portato alla scoperta
delle onde elettromagnetiche, con tutto ciò che segue. Nel caso della
meccanica newtoniana l'economicità della teoria non è evidente e, anzi, si
presta a varie critiche, come quelle espresse da Mach.
Ci si può chiedere poi se la II legge sia veramente una legge
fisica e non, piuttosto, una definizione di forza (o di massa, a seconda di
come si girano i termini dell'equazione). In realtà il problema è
essenzialmente formale, cioè riguarda le scelte "estetiche" nella formulazione
della teoria ma non il valore intrinseco della II legge di Newton. Quello che
conta, infatti, è la validità della teoria nel suo complesso, come insieme
coerente di definizioni e leggi. A titolo di esempio, si consideri la seguente
impostazione del problema (da D.V. Sivuchin, Corso di Fisica Generale,
ed. MIR): "Ogni descrizione del moto si riduce in fin dei conti alla
determinazione delle coordinate dei punti materiali del sistema meccanico come
funzioni del tempo. A questo scopo si deve ricorrere ad equazioni
differenziali dove, a fianco delle coordinate e delle velocità, figurano anche
le derivate delle velocità (o della quantità di moto) rispetto al tempo. Se il
punto materiale non è isolato, a causa delle interazioni con i corpi
circostanti la sua quantità di moto non si conserva. Così, tutto concorre a
caratterizzare l'effetto delle interazioni tramite la derivata della quantità
di moto rispetto al tempo, dp/dt. Una delle ipotesi fondamentali della
meccanica classica consiste nell'affermare che tale derivata dipenda dalla
posizione del punto materiale, in relazione alla posizione di tutti gli altri
corpi, ed anche, eventualmente, dalla sua velocità. Si può chiamare tale
funzione forza; se la indichiamo con F(r,v), si ha
dp/dt=F. Dunque, la derivata della quantità di moto di un punto
materiale rispetto al tempo è uguale alla forza alla quale è sottoposto".
Questo è l'enunciato della II legge di Newton, ma in questo caso il contenuto
fisico non sta tanto nell'equazione dp/dt=F, che è la
definizione di F, ma nell'affermare che F dipende solo da
r e v. Da questo punto di vista, lo scopo della meccanica è
essenzialmente la determinazione della forma di questa funzione in ogni caso
concreto. Resta il fatto che, per risolvere i problemi di moto dei punti
materiali, si deve disporre di equazioni differenziali che descrivano tali
moti. Il procedimento utilizzato per ottenere queste equazioni importa poco;
in particolare, esse possono essere ottenute senza ricorrere alla nozione di
forza.
Terza legge di Newton: Le azioni che due punti materiali
esercitano l'uno sull'altro sono uguali in modulo e dirette in senso opposto:
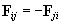 .
.
Legge di conservazione della quantità di moto: La quantità
di moto di un sistema isolato è costante. Questa è una delle leggi fondamentali
della natura che trova la sua origine nella omogeneità dello spazio. La legge di
conservazione della quantità di moto mostra che l'interazione tra i corpi che
compongono un sistema chiuso si riduce ad uno scambio di quantità di moto fra
questi corpi, ma non può variare il moto del sistema nel suo insieme intero,
qualunque sia il tipo di interazione.
Qui gli estensori del manuale dimenticano di dire che la III
legge di Newton (principio di azione-reazione) e la legge di conservazione
della quantità di moto sono equivalenti una volta accettata la seconda legge e
il principio di sovrapposizione. Infatti, applicando la seconda e la terza
legge a tutte le coppie di punti materiali che costituiscono un sistema
isolato, ne segue che la risultante delle forze è nulla e, quindi, la
variazione della quantità di moto è nulla. Viceversa, usando la seconda legge
e la conservazione della quantità di moto al caso di due soli punti materiali,
si ottiene che la costanza di p implica che la risultante delle forze è
nulla (somma vettoriale), cosa che equivale all'enunciato del principio di
azione-reazione. Si noti che il manuale dà maggiore enfasi alla legge di
conservazione della quantità di moto in quanto legata, come viene mostrato più
avanti, alla omogeneità dello spazio.
Apriamo qui una parentesi che riguarda la didattica. Visto lo
stretto legame tra il principio di azione-reazione e la conservazione della
quantità di moto, ci sembra corretto che le due cose vengano presentate
assieme, diversamente da quanto si fa in molti libri di testo, nei quali la
quantità di moto compare in un capitolo a parte, successivo agli enunciato
delle leggi di Newton. Il concetto di quantità di moto è necessario alla piena
comprensione della seconda e della terza legge di Newton. Uno dei problemi in
cui si incorre nel presentare la legge di azione-reazione da sola, senza la
conservazione di p, sta nella difficoltà di accettarne alcuni aspetti
contro-intuitivi. Ad esempio, è difficile convincere un studente,ai suoi primi
passi nella fisica, che una mela attrae la terra verso di sé con una forza
uguale alla forza peso con cui cade a terra. E simili ambiguità possono
nascere dal caso di reazioni vincolari su funi, pulegge e analoghi attrezzi
che abbondano negli eserciziari di fisica. Chiusa parentesi.
Tornando ai contenuti della terza legge (abbinata alla
conservazione di p) notiamo dapprima che essa non è contenuta nella
seconda, ma aggiunge nuove informazioni. La seconda legge serve soprattutto a
legare (o definire) i concetti di massa, forza e variazione di quantità di
moto, fornendo un metodo operativo (e matematico) per risolvere il problema
del moto data la massa e la forza. La terza invece stabilisce che le sole
forze interne ad un sistema non possono produrre un moto globale del sistema
stesso. Ciò è evidentemente legato alla omogeneità dello spazio (assenza di
punti privilegiati per la scelta dell'origine di un sistema di riferimento
generico). Un sistema isolato non ha alcun motivo di muoversi da sè verso
alcuna direzione, non esistendo alcun luogo privilegiato verso cui muoversi!
Una tale affermazione, corrisponde ad un ribaltamento della visione
geocentrica (ma anche eliocentrica, in senso stretto) e del concetto di luogo
naturale. Per questo motivo ha faticato ad emergere ed ha costituito, una
volta formalizzata nella terza legge, la chiave di volta per l'elaborazione di
una meccanica compiuta ed efficace. Ma le leggi di Newton non si limitano a
stabilire la non esistenza di luoghi naturali (una tale asserzione negativa
sarebbe priva di contenuti operativi), ma stabiliscono anche quale sia la
grandezza fisica che esprime operativamente questo concetto. L'impossibilità
di un moto globale di un sistema isolato viene tradotta nella costanza di una
quantità ben definita: il prodotto delle masse per le velocità dei corpi che
compongono il sistema. In questo senso, l'asserzione riguardo all'omogeneità
dello spazio non è più metafisica, ma diventa legge fisica.
Nel formulare la legge di azione-reazione Newton partì
sicuramente da alcuni dati istintivi. Quando si cerca di mettere in moto un
oggetto se ne ricava una resistenza. Quanto maggiore è la velocità a cui si
cerca di lanciarlo, tanto maggiore è la spinta che il nostro corpo riceve
all'indietro. Oppure, è impossibile sollevarsi in aria da sé tirando su la
propria sedia. Newton fece anche prove sperimentali, come quella di chiudere
in due vasetti un magnete e un pezzo di ferro, facendoli poi galleggiare in un
vaso d'acqua, per osservare come questi si avvicinavano l'un l'altro
raggiungendo una posizione di equilibrio. Si pose il problema di quale fosse
la relazione tra eguaglianza di azione e reazione (pressione e
contropressione) e la velocità impresse ai corpi. Se forze eguali producono
velocità inversamente proporzionali alla massa, allora l'azione reciproca tra
due corpi implica variazioni della quantità di moto uguali e opposte. Questo
suggerisce anche un metodo alternativo di definire la massa, misurando le
velocità di oggetti messi in moto dalla reciproca interazione.
Newton comprese che i concetti di massa e quantità di moto
erano, assieme alla seconda e la terza legge della dinamica, strettamente
connessi tra loro. Come dice Mach, "le esperienze che stanno a fondamento di
questi concetti sono: la conoscenza istintiva del rapporto tra pressione e
contropressione, il fatto che i corpi resistono alle variazioni di velocità
indipendentemente dal loro peso ma proporzionalmente a esso, l'osservazione
che i corpi di peso maggiore ricevono sotto uguale pressione velocità minori.
Newton ha capito bene quali concetti e princìpi base siano necessari alla
dinamica. è la forma della sua esposizione che lascia molto a desiderare."
Quest'ultima critica di Mach riguarda il criterio di
economicità della teoria di cui abbiamo già parlato precedentemente a
proposito della presunta ridondanza della legge di inerzia rispetto alla II
legge della dinamica. Ma, per evitare ogni eccesso di critica pro o contro la
posizione di "economicista", vale la pena notare che lo stesso Mach prosegue
dicendo che "con le nostre critiche non intendiamo in alcun modo sminuire il
valore dei lavori di Newton, poiché sappiamo che egli ha dovuto superare
difficoltà gravissime, ed è riuscito a superarle meglio di quanto avrebbe
potuto qualsiasi altro scienziato".
In ogni caso, Mach propone una formulazione della dinamica
completamente diversa identificando l'oggetto dell'indagine scientifica con lo
studio delle mutue relazioni tra i corpi, escludendo concetti esterni a tale
visione, come il tempo assoluto e lo spazio assoluto (in quanto concetti
metafisici, non fattuali), e partendo dall'accelerazione impressa ai corpi per
effetto dell'interazione reciproca, come evidenza sperimentale. La massa viene
allora definita tramite il rapporto di accelerazioni. Riguardo alla terza
legge di Newton, Mach sostiene che essa non contiene nulla di nuovo o, meglio,
è incomprensibile se non si possiede un concetto corretto di massa; ma una
volta che questo concetto sia stato formulato in base a esperienze dinamiche,
essa è inutile. Punto centrale della critica è dunque la definizione di massa;
ricorrere all'idea di "quantità di materia" è per Mach una procedura estranea
alla scienza, in quanto equivale ad assumere rappresentazioni che a loro volta
hanno bisogno di essere giustificate. La vera definizione di massa può essere
ottenuta solo prendendo in considerazione le relazioni dinamiche dei corpi.
Basandosi su tale visione della dinamica e, più in generale, della scienza,
Mach arrivò all'eccesso (almeno se giudicato a posteriori) di negare validità
ad ogni ipotesi atomistica della materia, anche in presenza di convincenti
argomenti teorici e sperimentali a sostegno dell'esistenza degli atomi.
Dunque, come Newton era condizionato da pregiudizi metafisici inevitabili per
l'epoca, Mach finisce per essere condizionato da pregiudizi metodologici la
cui rigidità contrasta, altrettanto inevitabilmente, con la molteplicità dei
percorsi seguiti dalla scienza nel suo progredire.
Un problema profondo, legato al significato della III legge,
è quello dell'azione a distanza, ovvero: come le varie parti di un sistema
isolato si comunicano le variazioni locali di configurazione, e quindi le
variazioni delle forze in gioco tra le parti del sistema. Questo problema ha
costituito uno dei nodi cruciali della meccanica e merita di essere
approfondito. Il punto di partenza è l'osservazione che le forze possono agire
a distanza, senza intervento di un mezzo intermediario. Questo è vero, ad
esempio, per la forza gravitazionale e le forze elettromagnetiche, che si
esercitano tra corpi separati da uno spazio "vuoto". Se si vuole garantire
validità alla legge di conservazione della quantità di moto (e quindi, del
principio di azione e reazione) bisogna intendersi su cosa significa la parola
"vuoto".
Cominciamo con l'assumere un punto di vista meccanicista
primitivo e supponiamo che un corpo A e un corpo B interagiscano tra loro
senza che tra essi via sia contatto. Per assenza di contatto intendiamo qui
che non vi sono tra A e B altri corpi meccanici, dotati di massa, siano essi
solidi, fluidi, elastici, o quant'altro. Ad esempio, A e B possono essere la
terra e la luna che interagiscono secondo la legge di attrazione
gravitazionale, oppure due cariche elettriche che si attraggono o si
respingono secondo la legge di Coulomb. Allora, se si assume come valida la
legge di conservazione della quantità di moto, si conclude che l'interazione
tra A e B avviene istantaneamente e ogni informazione sui cambiamenti della
disposizione reciproca si propaga a velocità infinita. Se così non fosse,
infatti, il corpo A potrebbe muoversi dalla sua posizione iniziale senza che B
se ne accorga, per un intervallo di tempo pari al tempo necessario alla
propagazione dell'informazione da A a B. Durante questo tempo la quantità di
moto del sistema non sarebbe conservata. In termini della terza legge di
Newton, possiamo dire che durante tale intervallo di tempo la "reazione" di B
sarebbe diretta ancora verso la posizione iniziale di A, non avendo B alcuna
informazione sulla nuova posizione, in tal modo violando la terza legge
stessa. Fintanto che non esistono misure sulla velocità di propagazione
dell'interazione, questa impostazione è legittima e non si hanno problemi
nemmeno con la definizione di vuoto.
Ora, si tenga presente che la teoria sull'elettromagnetismo,
formulata nel XIX secolo e confermata sperimentalmente, prevede una velocità
di propagazione dell'interazione pari alla velocità della luce, grande ma non
infinita. Ciò pone di fronte a una scelta: 1) si continua a ritenere che
l'interazione si propaghi in assenza di corpi materiali intermediari, ma si
ammette che la terza legge di Newton non è più vera, oppure 2) si continua a
ritenere vera la terza legge di Newton ma si ipotizza l'esistenza di un mezzo
meccanico che riempia lo spazio tra A e B e che si faccia carico del trasporto
della quantità di moto durante la propagazione dell'interazione.
Ai fisici del XIX secolo, l'eventualità di dover abbandonare
la III legge di Newton (e il principio di conservazione della quantità di
moto) dev'essere sembrata terribilmente dolorosa. Hanno preferito introdurre
o, meglio, rielaborare il concetto di "etere", identificando con esso il mezzo
materiale che permea tutto lo spazio e che trasmette le interazioni tra i
corpi. Il nuovo problema che si pone, a quel punto, è come verificare
sperimentalmente l'esistenza dell'etere in modo indipendente, ovvero porre il
problema dell'etere su un piano quantitativo, caratterizzandone le proprietà
in termini di quantità misurabili. Malgrado numerosi sforzi in questa
direzione, l'etere non è mai stato osservato.
Ma allora, torniamo indietro a quanto detto sulla necessità
di introdurre un mezzo meccanico che trasporti la quantità di moto nel
processo di interazione tra A e B: possiamo rinunciare all'idea che questo
trasporto avvenga tramite un "mezzo meccanico"? La risposta è sì, ma richiede
l'introduzione di "qualcosa d'altro", in grado di produrre lo stesso effetto.
Per questo è stato introdotto il concetto di "campo". In effetti fu proprio
Maxwell ha scoprire che le leggi dell'elettromagnetismo trovavano la loro
espressione naturale nelle equazioni differenziali del campo elettrico e del
campo magnetico. Ma per alcuni decenni, data la visione meccanicista
imperante, si tentò di dare alle oscillazioni del campo (onde
elettromagnetiche che si propagano alla velocità della luce) un "supporto
meccanico", l'etere appunto. Infine, ci si convinse che tale "portatore" di
onde non esisteva, e il "campo" assunse il ruolo di concetto elementare
autonomo, valido anche nel caso degli altri tipi di interazione.
Schematicamente, il corpo A provoca, nello spazio circostante, un campo di
forze che si manifesta attraverso una forza agente su B. Anche il corpo B
origina un campo analogo che agisce su A. L'interazione è quindi mediata da un
campo; si parlerà di campo gravitazionale, elettromagnetico, ecc. Le stesse
interazioni di contatto, in realtà, sono l'effetto di campi che agiscono su
piccole distanze (campi molecolari, a loro volta riconducibili a campi
elettrici). Perturbazioni dei campi (ad esempio, a seguito del movimento di
una delle sorgenti) si propagano ad una velocità finita, ma ad ogni campo è
associata una certa quantità di moto in modo che la legge di conservazione
della quantità di moto (e la III legge di Newton) rimane valida.
Il campo appare dunque come la soluzione al problema
dell'azione a distanza, implicita nella dinamica newtoniana. Ma vale la pena
sottolineare almeno un paio di questioni che esso apre. La prima è una
possibile ambiguità di tipo "nominalista". Siamo sicuri che l'abbandono
dell'etere a favore del campo non sia solo una questione di terminologia? La
risposta, ovviamente, è che etere e campo sono sostanzialmente diversi
nell'insieme delle proprietà che li caratterizzano e altrettanto diversi nella
visione stessa di realtà fisica che essi sottintendono. Ciò che i fisici del
XIX secolo chiamavano etere era una sostanza avente un comportamento meccanico
analogo a quello dei corpo ordinari. Si poteva cioè parlare del suo stato di
quiete e di moto, della sua densità, elasticità, delle forze agenti su di
esso. Si poteva persino usarlo come sistema di riferimento, come un corpo
qualsiasi che si trovi immerso nello "spazio assoluto". Tutto ciò non ha alcun
significato per i campi. Il campo è una nuova entità fisica, non meccanica,
che media l'interazione tra le particelle e che trasporta energia e quantità
di moto. Le proprietà che i fisici moderni associano al concetto di campo sono
compatibili con una gran mole di osservazioni sperimentali. C'è di più: l'idea
di etere era del tutto compatibile con l'esistenza di uno "spazio assoluto",
implicito nella dinamica newtoniana, mentre l'idea moderna di campo non lo è.
Il concetto di spazio separato da ogni contenuto fisico non esiste. La realtà
fisica dello spazio è essa stessa rappresentata dai campi. Detto questo, non
si vede come il passaggio dall'etere ai campi possa essere ridotto ad una
questione di terminologia.
La seconda questione, più profonda, è che l'introduzione del
concetto di campo ha prodotto anche una certa incoerenza nella teoria della
dinamica, associata alla natura continua o discreta dello spazio. Ad esempio,
la teoria di Maxwell, anche se descrive in maniera soddisfacente il
comportamento delle particelle cariche elettricamente nelle loro interazioni
reciproche, non spiega il comportamento delle densità di carica, cioè non
fornisce una descrizione delle particelle stesse, che devono essere trattate
quindi come oggetti puntiformi. La combinazione dell'idea di un campo continuo
con quella di punti materiali discontinui nello spazio appare incoerente. Una
teoria dei campi coerente richiede la continuità di tutti gli elementi della
teoria, non soltanto nel tempo ma anche in tutti i punti dello spazio. Di
conseguenza la particella "materiale", in senso newtoniano, non trova posto
come concetto fondamentale nella teoria dei campi. Purtroppo, una trattazione
anche parziale di questo problema richiede nozioni di fisica moderna che
esulano dagli scopi di questo corso.
Legge fondamentale del moto di traslazione: la derivata
temporale della quantità di moto di un sistema di punti materiali, in un sistema
di riferimento inerziale, è uguale alla risultante delle forze esterne applicate
al sistema. In forma matematica:
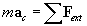 ,
,
dove ac è l'accelerazione del centro di
massa. Per questo motivo, il moto di un corpo esteso, per quanto riguarda la sua
traslazione, può essere ridotto al moto di un punto materiale posto nel suo
centro di massa e su cui agisce la risultante delle forze esterne.
Il principio di relatività (in meccanica classica): La
relazione esistente tra le coordinate e i tempi, relativi a due sistemi di
riferimento inerziali arbitrari, è data dalle trasformazioni di Galileo:
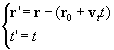
dove vt è la velocità relativa, costante, dei
due sistemi di riferimento e r0 è la distanza tra le origini
dei due sistemi al tempo t0. La seconda relazione esprime il
carattere assoluto del tempo in meccanica classica, il fatto cioè che il tempo
scorre in maniera identica in tutti i sistemi di riferimento inerziali.
Le trasformazioni di Galileo sono tali che l'accelerazione di
un punto materiale qualsiasi soggetto ad una data forza è la stessa in tutti i
sistemi di riferimento inerziali:
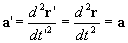
e quindi F'=F.
Le leggi del moto sono quindi invarianti rispetto alle trasformazioni di
Galileo.
Il principio di relatività così formulato garantisce, tra
l'altro, il fatto che il moto uniforme di un sistema chiuso non ha alcuna
influenza sui processi meccanici interni al sistema. Questa era proprio la
motivazione di Galileo, ben espressa nell'esempio degli esperimenti compiuti
nella stiva della nave in moto, raccontata nei Dialoghi sopra i massimi
sistemi. L'esempio serviva a convincere gli scettici a proposito della
rotazione della terra.
Il principio di relatività è indispensabile per garantire
l'applicabilità delle leggi della meccanica (delle stesse leggi!) in sistemi
di riferimento diversi. L'invarianza delle leggi fisiche rispetto al
cambiamento del sistema di riferimento è uno dei requisiti di ogni teoria
sensata. Essa ha a che vedere con il passaggio dalla visione soggettiva alla
visione intersoggettiva o, in altri termini, alla comunicabilità delle
esperienze, in forma di numeri e leggi, tra diversi osservatori. Se una teoria
non soddisfa tale requisito, possono essere sbagliate le sue leggi o possono
essere sbagliate le leggi di trasformazione delle coordinate, ma non si può
rinunciare, in ogni caso, al requisito di invarianza. Così, il fatto che la
teoria di Maxwell per l'elettromagnetismo preveda la propagazione di onde a
velocità c e che questa velocità risulti essere la stessa in tutti i
sistemi di riferimento ha portato ad una modifica sostanziale sia delle leggi
della dinamica, sai delle leggi di trasformazione (Lorentz anziché Galileo).
Infine si noti che il principio di relatività esclude
l'esistenza di un singolo sistema di riferimento privilegiato (sistema
"assoluto"); tutti i sistemi inerziali sono equivalenti. Tuttavia la meccanica
newtoniana si basa ancora sull'ipotesi che esista un "tempo assoluto", che
scorre allo stesso modo in tutti i sistemi di riferimento. L'abolizione del
tempo assoluto si renderà necessaria quando si imporrà l'invarianza della
velocità della luce, come nella teoria della relatività ristretta. L'ulteriore
generalizzazione (relatività generale) consisterà nell'inclusione dei sistemi
non inerziali in un principio di relatività.
Moto in sistemi non inerziali: benché le leggi di Newton
siano valide solamente per il moto nei sistemi inerziali (il principio di
inerzia vale solo nei sistemi inerziali per definizione), la II legge può essere
utilizzata formalmente anche per un sistema non inerziale di cui si conosca
l'accelerazione rispetto ad uno inerziale. In tal caso, infatti, la
trasformazione dell'accelerazione dal sistema inerziale a quello non inerziale
introduce uno o più termini aggiuntivi, dovuti al moto accelerato di traslazione
del sistema o alla rotazione degli assi. Moltiplicando tali accelerazioni per la
massa del corpo di cui si studia il moto, si ottengono delle grandezze aventi le
dimensioni di forze. La II legge, nel sistema non inerziale, è quindi
formalmente identica a quella valida per il sistema inerziale, salvo includere
le forze "fittizie" derivanti dal moto accelerato del sistema di riferimento
(forza fittizia di trascinamento, forza centrifuga, forza di Coriolis).
L'applicazione della II legge di Newton al caso dei sistemi
non inerziali non deve essere fraintesa. Quando si dice che la II legge di
Newton è applicabile al moto nei sistemi non inerziali introducendo delle
forze fittizie, non si intende che essa sia "valida" in quei sistemi. Essa
rimane valida solo nei sistemi inerziali. La possibilità di utilizzarla anche
al di fuori di questi richiede una assunzione fondamentale: conoscere
l'accelerazione del sistema non inerziale rispetto ad un sistema inerziale
assegnato. In tal modo, date le forze (vere) agenti su un corpo, si può
dapprima scrivere la II legge nel sistema inerziale, per calcolare la derivata
seconda del vettore r, e poi riscrivere la stessa equazione in termini
del vettore r' riferito al sistema non inerziale. Dato che il tempo è
lo stesso nei due sistemi, l'equazione avrà la stessa forma, ma con dei
termini in più, che chiameremo forze fittizie. La separazione esplicita tra
forze vere e forze fittizie è possibile solo se l'accelerazione del sistema
non inerziale, rispetto a quello inerziale è nota. Nell'ambito della meccanica
classica, i sistemi inerziali rimangono quindi privilegiati, dato che per
descrivere il moto di un corpo in un sistema inerziale non è necessaria alcuna
informazione sul moto relativo ad altri sistemi esterni ad esso.
La legge di attrazione universale: Fra tutte le coppie di
punti materiali agiscono forze di mutua attrazione che sono proporzionali alla
massa di questi punti ed inversamente proporzionali al quadrato delle loro
distanza:

dove u12 è un vettore unitario nella
direzione della congiungente i due punti. Il valore numerico della costante
dipende dalle unità di misura utilizzate per masse, distanze e forze.
La forza di attrazione ha la stessa forma anche per due corpi
sferici; in tal caso la distanza che appare nell'espressione della forza è la
distanza tra i due centri. Così pure è valida per un corpo di forma qualsiasi
attratto da una sfera, nel caso in cui il raggio della sfera sia molto maggiore
delle dimensioni del corpo in questione. Questo è anche il caso degli oggetti
posti in prossimità della superficie terrestre, per i quali vale
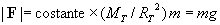
dove MT e RT sono, rispettivamente, la
massa e il raggio della terra. La nuova costante g ha le dimensioni di una
accelerazione (distanza su tempo al quadrato) e viene chiamata accelerazione di
gravità. Si noti che l'accelerazione di gravità è la stessa per tutti i corpi.
Il fatto che un corpo qualsiasi cade sulla superficie della terra con
accelerazione g segue dall'equivalenza della massa gravitazionale e della
massa inerziale; solo in tal caso infatti, inserendo l' espressione della forza
di gravità nella seconda legge di Newton, la massa scompare dal risultato.
L'attrazione gravitazionale è una delle interazioni
fondamentali in natura. Un'altra, ad esempio, è l'interazione elettromagnetica
che per due cariche elettriche in quiete ha esattamente la stessa forma della
forza gravitazionale tra due masse, salvo sostituire le due masse con le due
cariche e adattare la costante alle nuove unità di misura. Altre interazioni
fondamentali sono le cosiddette interazioni forti e deboli (il nome, in questo
caso, non aiuta molto). In un manuale "standard", la forza gravitazionale
compare assieme all'esposizione dei fondamenti della meccanica. La ragione
storica è che, effettivamente, si tratta della prima esplicitazione del
concetto di forza, fatta da Newton stesso, al fine di mostrare la validità
delle leggi della meccanica quando applicate sia ai moti astronomici che alla
caduta dei gravi.
C'è un'altra ragione per cui la forza gravitazionale appare
strettamente connessa alle leggi della dinamica: il fatto che la forza agente
su un corpo per effetto dell'attrazione gravitazionale sia proporzionale alla
sua massa e, più precisamente, alla stessa massa che compare nella II legge di
Newton. E' ben vero che avremmo potuto scrivere la formula per l' attrazione
gravitazionale, modificando opportunamente la costante a secondo membro, in
termini del prodotto di due grandezze fisiche diverse, diciamo due "cariche"
gravitazionali Q1 e Q2; ma questo sarebbe solo un cambio
formale, dato che poi la verifica sperimentale ci avrebbe fornito una nuova
legge: la carica gravitazionale Q è uguale alla massa m a meno di un fattore
moltiplicativo arbitrario. Questa legge, quando si scelga la costante uguale a
1, corrisponde all' equivalenza della massa inerziale e della massa
gravitazionale.
È difficile pensare che questo fatto sia accidentale. Si può
piuttosto immaginare che esso segua da una struttura "intrinseca" dello spazio
(o spazio-tempo) in cui si trovano i corpi. La soluzione di questo problema,
nell'ambito della relatività generale, passa attraverso il principio di
equivalenza, formulato nel modo seguente. Sia le forze gravitazionali che le
forze fittizie (d'inerzia) in un sistema di riferimento accelerato sono
proporzionali alla massa del punto materiale di cui si studia il moto. Ne
segue che il moto libero di un corpo, rispetto ad un sistema di riferimento
non inerziale, è identico al moto dello stesso corpo rispetto ad un sistema di
riferimento inerziale sotto l'azione di una certa forza gravitazionale
equivalente. Questo è il punto di partenza della teoria della relatività
generale, che comporta una re-interpretazione dello spazio-tempo e un
superamento della fisica classica.
Tornando a Newton, egli riuscì a scrivere un'espressione
della forza gravitazionale che, una volta inserita nelle equazioni del moto,
spiegava sia le orbite dei pianeti, sia la caduta dei gravi, sia molti altri
fatti ancora: questa fu l'origine del suo grande successo. Ma Newton aveva
anche buone ragioni per essere insoddisfatto. L'equivalenza tra massa
inerziale e massa gravitazionale si presentava, nella sua teoria, come una
legge aggiuntiva e, ancor più grave, egli non riuscì a fornire alcuna
informazione sulla "causa" della gravità. Dobbiamo tener presente che Newton
era un "essenzialista" (si veda il precedente commento alla definizione di
massa) e il suo fine era quello di arrivare ad una spiegazione ultima dei
fatti, basata sull'"essenza" delle cose. Così l'inerzia e la massa potevano
essere considerate proprietà essenziali dei corpi materiali. La forza
gravitazionale, invece, non poteva esserlo, in quanto aveva a che fare con
proprietà "relazionali", interazioni tra un corpo e un altro corpo (non era
una proprietà "vera" di un corpo, dato che dipendeva dall'esistenza di altri
corpi). Dunque, per giungere allo scopo ultimo della teoria, la forza
gravitazionale doveva ancora essere ricondotta ad una causa più profonda.
Newton non riuscì in tale progetto, e nemmeno tentò nuove ipotesi ad hoc
("hypotheses non fingo"). Questo non impedì ai suoi successori, più newtoniani
di Newton, di forzare la mano, mostrando che la teoria del loro maestro era
sufficiente a dare la spiegazione ultima. Il capostipite di questa visione fu
Roger Cotes, autore della prefazione alla seconda edizione dei
Principia di Newton, il quale propose di aggiungere all'essenza di un
corpo materiale la proprietà di attrarre gli altri corpi (gravità). Ciascun
corpo era così dotato di un potere di attrarre (gravità) e di un potere di
resistere (inerzia), ed essendo entrambe queste proprietà inerenti allo stesso
corpo dovevano essere proporzionali alla stessa massa. Dunque, l'equivalenza
tra massa inerziale e gravitazionale non è più, entro questa visione,
un'ipotesi aggiuntiva. Inoltre, la gravità deve irradiarsi da ciascun corpo e
l'effetto di attrazione reciproca di due corpi dovrà essere proporzionale al
prodotto delle masse. Questa spiegazione ultima dei fatti è coerente con
l'impostazione essenzialista di molti newtoniani e fu dominante per lungo
tempo al punto da assumere carattere dogmatico. Anche per questo motivo vi fu,
nell'800, chi reagì a questo dogmatismo essenzialista con un opposto
dogmatismo anti-essenzialista, come Mach. Al giorno d'oggi si tende a porre la
questione in altri termini: la forma che diamo alle forze fondamentali,
nell'ambito delle teorie fisiche correnti, è finalizzata non ad una
"spiegazione ultima" ma ad una "rappresentazione migliore" di ciò che accade
in natura, avendo in mente alcuni sani criteri per valutare quando e quanto
una rappresentazione sia migliore di un'altra.
3. Lavoro, energia meccanica ed elementi di meccanica
analitica
Energia: si chiama energia quella grandezza fisica che
permette di valutare in maniera univoca le diverse forme di moto. L'energia è
una grandezza scalare. Per poter dare una valutazione quantitativa delle forme
di moto qualitativamente diverse che si trovano nella fisica, si introducono le
diverse forme di energia: meccanica, interna, elettromagnetica, nucleare,
ecc.
Una definizione del genere può avere senso compiuto solo se
accompagnata da una visione generale dei problemi del moto, che prescinde, in
qualche modo, dalla definizione stessa. Presa da sola, la definizione risulta
priva di significato.
Legge di conservazione dell'energia: quali che siano i
processi che avvengono in un sistema isolato, la sua energia totale non cambia
nel tempo.
Questa legge è una delle più importanti della natura ed è
conseguenza della omogeneità del tempo.
È la seconda volta che si invoca una ipotesi di omogeneità.
Nel caso della conservazione della quantità di moto si invocava l'omogeneità
dello spazio. Per l'energia invece si tratta di omogeneità del tempo (non
esiste alcun istante privilegiato per la scelta dell'origine dei tempi in un
sistema di riferimento).
Dato che qui la legge di conservazione non appare derivata da
altre leggi, lo scopo degli estensori del manuale era probabilmente quello di
mettere subito in evidenza il punto d'arrivo delle definizioni e dei concetti
trattati di seguito. Il percorso storico (lungo e accidentato, per inciso) è
passato invece attraverso le definizioni delle singole forme di energia in
termini delle quantità note precedentemente e le leggi di conservazione
parziali che si possono ottenere osservando singole classi di processi.
Uno di questi passaggi, che ha giocato un ruolo chiave nella
storia della fisica, è l'identificazione del calore come una forma di energia
e la derivazione di un principio di conservazione che includa sia l'energia
meccanica che il calore (I principio della termodinamica). Ma problemi simili
sono stati affrontati anche in epoche più recenti, come nel caso dell'
apparente violazione della conservazione dell'energia nelle prime osservazioni
della radioattività naturale. è ben noto, poi, che energia e massa si
ritrovano unite, con la teoria della relatività, in un'unica legge di
conservazione (la fin troppo nota E=mc2 !).
Un aspetto che vale la pena sottolineare qui è che il
concetto di energia è entrato a far parte della fisica intorno alla prima metà
dell'ottocento e non è certo accidentale il fatto che, nello stesso periodo,
si abbia la rivoluzione industriale, con le sue macchine, il lavoro,
l'efficienza, il guadagno, e così via. Il linguaggio della fisica non è certo
estraneo a quello che succede nell'ambito delle altre attività umane.
Lavoro: il lavoro elementare eseguito da una forza è dato
dal prodotto scalare della forza stessa per lo spostamento infinitesimo del suo
punto di applicazione:
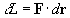 .
.
Il lavoro compiuto su un percorso tra due punti generici A e B
è l'integrale del lavoro elementari lungo lo stesso percorso.
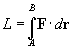 .
.
L'integrale può dipendere, in generale, dalla scelta del
percorso tra i due punti assegnati. In tal caso il lavoro elementare non è un
differenziale esatto. Se invece il lavoro elementare è un differenziale esatto,
allora il lavoro non dipende dalla scelta del percorso (dL=dL) e la forza è detta forza potenziale. Nel caso di forze
che non dipendono esplicitamente dal tempo, la forza potenziale è detta anche
conservativa.
La potenza è il lavoro eseguito nell'unità di tempo
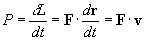 .
.
Forze conservative ed energia potenziale: nel caso di forze
che non dipendono dal tempo, la condizione che esse siano conservative è
equivalente ad assumere che il lavoro eseguito lungo un percorso chiuso
qualsiasi è identicamente nullo:
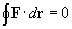 .
.
Affinché si realizzi questa condizione è necessario e
sufficiente che l'integrando sia il differenziale esatto di una certa funzione
scalare delle coordinate, nella forma:
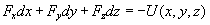 ,
,
dove il segno meno è stato introdotto per convenzione. La
quantità U(x,y,z) così definita viene chiamata energia potenziale.
Dall'espressione precedente segue anche:
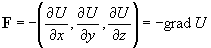 .
.
Così, il lavoro svolto da una forza conservativa spostando un
punto materiale da A a B vale
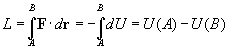 .
.
L'energia potenziale è la forma di energia che dipende dalla
configurazione del sistema, cioè dalla disposizione reciproca delle particelle
del sistema e dalla loro posizione rispetto ad un campo di forze esterne. Tale
energia è misurata tramite il lavoro che le forze conservative (interne ed
esterne) compiono nel passaggio da una configurazione assegnata ad una
configurazione di riferimento, a cui si associa arbitrariamente energia
potenziale nulla (U(B)=0, nella formula precedente, se B è la configurazione di
riferimento).
Energia cinetica: l'energia cinetica è il lavoro che un
corpo può compiere quando il suo moto sia frenato fino all' arresto totale. A
partire dalle leggi di Newton si mostra che tale lavoro, nel caso di un singolo
punto materiale, è dato da
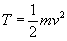 .
.
Energia meccanica: l'energia meccanica di un punto
materiale è data dalla somma dell'energia cinetica e dell'energia potenziale,
E=T+U. Per un sistema di punti materiali, l'energia totale è la somma delle
energie dei singoli punti.
Se tutte le forze che agiscono sul sistema sono conservative,
l'energia meccanica è costante nel tempo (principio di conservazione
dell'energia meccanica).
Un sistema è detto, invece, dissipativo quando la sua energia
meccanica diminuisce nel tempo in conseguenza della trasformazione in altre
forme (non meccaniche) di energia (ad esempio, calore).
Cartesio nel 1644 scriveva: "è del tutto razionale ritenere
che Dio, poiché all'atto della creazione della materia impartì differenti moti
alle sue parti, e poiché conserva tutta la materia nello stesso modo e nelle
stesse condizioni in cui la creò, nello stesso tempo conservi in essa la
quantità di moto". Per Cartesio, come successivamente per Newton, la quantità
di moto è il prodotto della massa di un corpo per la sua velocità.
Leibniz (1646-1716) pure credeva che nel moto dei corpi
qualcosa dovesse conservarsi, ma non era d'accordo sul fatto che la grandezza
conservata fosse la quantità di moto. Per lui a conservarsi doveva essere la
forza (vis), ma non la forza inclusa nelle leggi di Newton, posteriori a
Leibniz stesso, ma una forza "che deve essere valutata dalla quantità
dell'effetto che produce, per esempio dall'altezza a cui può innalzare un
corpo pesante e non dalla velocità che può imprimergli". In base a questo
ragionamento egli introdusse una vis viva data dal prodotto della massa
per il quadrato della velocità! La forza impressa ad un sasso lanciato verso
l'alto doveva essere in qualche modo immagazzinata; quando il sasso raggiunge
il massimo di altezza, la velocità si annulla ma la forza (nel nostro
linguaggio, l'energia meccanica) deve rimanere nel sasso in altra forma.
Huygens, in base ad uno studio sugli urti tra corpi, fece osservare a Leibniz
che il prodotto mv2 diminuisce in seguito agli urti, invece di
rimanere costante. Ma Leibniz rimase convinto della conservazione della vis
viva, e per giustificarne l'apparente diminuzione suggerì che essa venisse
parzialmente suddivisa nelle "piccole parti" che costituiscono i corpi.
Questo concetto, peraltro estremamente efficace se giudicato
a posteriori, rimase per molto tempo dietro le quinte. Una ragione di questo
sta nel fatto che Newton, contemporaneo di Leibniz e Huygens, formulò la sua
teoria a partire dal concetto di forza, e non da quello di energia, fornendo
una soluzione al problema del moto in termini di equazioni differenziali, e
non in termini di quantità conservate. Questo rimase lo schema vincente per
molto tempo. Un'altra ragione è il fatto che mancavano osservazioni
sperimentali a sostegno dell'idea di Leibniz, almeno fino alla formulazione
della teoria cinetica dei gas, intorno alla metà dell'800. A quell'epoca
l'energia era tornata di moda anche per opera di quei fisici, come Langrange e
Hamilton, che svilupparono la meccanica analitica. Inoltre, lo stesso concetto
era entrato prepotentemente nelle discussioni intorno alla termologia e la
termodinamica (anche, come si è già detto, sostenuto dalle nuove necessità
della rivoluzione industriale). Il suo merito maggiore, in quel contesto, era
quello di permettere l'unificazione di teorie fino ad allora distinte quali
erano la meccanica newtoniana dei corpi materiali e la teoria del calore. Un
effetto di questa unificazione fu la progressiva sparizione del "fluido
calorico" dalle teorie fisiche.
In effetti, uno dei criteri comunemente accettati per
stabilire se una teoria è migliore di un'altra è quello di considerare la
capacità di una teoria di unificare concetti diversi in uno stesso schema
interpretativo. In questo senso, la teoria fisica che emerge dalla meccanica
newtoniana una volta aggiunto per bene il concetto di energia (inclusi i
fenomeni termici) è una teoria migliore, rispetto alla formulazione newtoniana
originaria. Il cardine di tale teoria diventa il principio di conservazione
dell'energia. I fisici dell'800 videro in questo progresso conoscitivo un
segno che la loro scienza era davvero potente e che si era vicini ormai ad una
descrizione completa della realtà basata sulla meccanica newtoniana e sul
concetto di energia. Si svilupparono tendenze estreme in questo senso, come
quella della cosiddetta "energetica", secondo cui tutte le leggi dovrebbero
essere unificate in un'unica legge di conservazione dell'energia, essendo
compito del fisico quello di classificare, per ciascun fenomeno, cosa sia
energia cinetica e cosa sia energia potenziale. Uno dei maggiori esponenti di
questa corrente era Wilhelm Ostwald, il quale arrivava a negare qualsiasi
esistenza della materia (la materia non esiste) a favore dell'energia, con
questo interpretando, in modo alquanto forzato, la negazione dell'essenza
delle cose già formulata da Mach (il quale negava sì l'esistenza degli atomi,
ma anche dell'energia, per la stesse ragioni). Ostwald era ottimista nella sua
visione della realtà al punto da ipotizzare che l'energia governasse anche
fenomeni al di fuori del campo abituale della fisica, come le questioni legate
alla psicologia e alle spirito in senso lato. Ad esempio, propose una
definizione di felicità in termini energetici, come la differenza tra il
quadrato di E e il quadrato di W, essendo E l'energia spesa intenzionalmente e
con successo, W quella spesa con disgusto.
Si era ormai a cavallo tra l'800 e il '900, e Boltzmann aveva
difficoltà a far accettare la sua meccanica statistica, preludio alla fisica
moderna. Come diceva Planck: "Negli anni '80 e '90 del secolo scorso,
un'esperienza personale m'ha insegnato quanto a un ricercatore, in possesso di
un'idea, sulla quale ha maturamente riflettuto, costasse cercare di
propagarla. Constatava quanto i migliori ragionamenti che esibiva a tal fine,
pesassero poco, perchè la sua voce non aveva l'autorità sufficiente di imporla
al mondo della scienza. In quell'epoca era vano tentare di contrastare i
Wilhelm Ostwald, i Georg Helm, gli Ernst Mach". Nelle conferenze
internazionali dell'epoca era Ostwald, e non Boltzmann, ad avere la meglio,
malgrado le sue idee ci sembrino, oggi, assai carenti sia nel contenuto che
nel metodo.
Ci si può chiedere come mai una corrente di pensiero
vistosamente inadeguata (non solo se giudicata col senno di poi, ma anche con
quello dell'epoca) possa godere di un tale successo. Una delle cause, anzi,
probabilmente la causa principale, è il fatto che le idee dell'energetica
erano semplici e di facile presa. Viste con una mente critica, esse appaiono
semplici in quanto superficiali, nel senso che un'indagine più approfondita ne
mostrerebbe facilmente le pecche. Ma il destinatario del messaggio non sempre,
o piuttosto raramente, sa cogliere la connessione tra semplice e superficiale,
preferendo di solito associare "semplice" a "bello" e, di là, anche a "vero".
Se chi ascolta una relazione scientifica viene posto nella condizione di
capire un concetto semplice (la conservazione dell'energia) e viene pure
convinto che tale concetto unifica le conoscenze, al punto da porsi come
risposta ultima ai problemi della fisica (e non solo di quella), ne sarà
sicuramente gratificato e loderà il relatore (in quanto capace di esprimere
concetti difficili in un linguaggio semplice). Poco importa se quel concetto è
solo uno degli elementi di un quadro più complicato, non libero da
contraddizioni e da problemi irrisolti. Il messaggio semplice e gratificante
si amplifica facilmente proprio in quanto superficiale. L'energetica si presta
come caso esemplificativo di una prassi frequente, sia nella scienza che in
altre discipline. Se le teorie migliori emergono comunque, magari con un po'
di fatica in più, questo è dovuto al fatto che la scienza procede con una
metodologia sostanzialmente sana, basata sulla critica continua delle
convinzioni assodate, la formulazione di congetture sempre più profonde e
verificabili. Resta però sempre vivo il problema delle comunicazione delle
teorie e dei risultati della scienza ad un pubblico vasto, fatto sia di
persone incompetenti (in quanto competenti in qualcosa d'altro) che competenti
(ma non al punto da cogliere tutti i dettagli). La cosiddetta divulgazione
scientifica soffre infatti del problema della "semplificazione" del messaggio,
e non sempre ne esce bene.
Il fatto che la conservazione dell'energia non possa essere
il mattone unico con cui costruire le teorie fisiche, come avrebbero voluto i
sostenitori dell'energetica, si comprende alla luce delle seguenti
considerazioni. La prima è che la conservazione dell'energia non spiega
l'esistenza di processi irreversibili, quelli che stanno alla base del secondo
principio della termodinamica. Per dare un'interpretazione adeguata ai
processi irreversibili bisogna ricorrere a leggi aggiuntive di tipo
statistico. Questo fece, tra gli altri, Boltzmann, il quale diede un
significato ben preciso della grandezza "entropia" in termini di disordine
microscopico. Dunque, come minimo, la legge di conservazione dell'energia va
affiancata da una legge che sancisca l'aumento dell'entropia in ogni processo
spontaneo. La seconda questione riguarda il fatto che, alla luce della
relatività speciale di Einstein, energia e massa non possono essere
considerati concetti distinti e la legge di conservazione dell'energia deve
essere riformulata totalmente, a favore di una conservazione di massa-energia.
La terza questione, infine, riguarda il fatto che, secondo la meccanica
quantistica, la conservazione dell'energia non è sempre garantita; possono
avvenire processi in cui la conservazione dell'energia è violata di una
quantità (delta E) per un certo intervallo di tempo (Delta t), purche' il
prodotto (Delta E)(Delta t) sia minore di una costante dell'ordine della
costante di Planck (circa 10^(-27) erg sec). In questo modo, ad esempio, si
spiega un fenomeno come l'effetto tunnel (ovvero il fatto che una particella
possa superare una barriera di potenziale pur avendo un'energia meccanica
minore di quella necessaria per uno scavalcamento classico, compatibile con la
conservazione dell'energia). Tale fenomeno è frequente in natura e sta alla
base del cosiddetto "microscopio ad effetto tunnel".
Una volta ricollocata l'energia al suo giusto posto, peraltro
importante, ritengo utile fare un'ultima considerazione, un po' a margine, che
riguarda ancora l'energetica ma in chiave odierna. L'uso del termine "energia"
nel linguaggio corrente è molto frequente e altrettanto vario. Capita spesso
di sentirlo associato a questioni metafisiche, psicologiche,
para-psicologiche, new-age, eccetera. Si parla di energie positive o negative
che si sprigionano, si concentrano qua e là, fluttuano. Pare che il saper
controllare questi flussi di energia sia una delle competenze più richieste
dal mercato, a giudicare dal giro d'affari che muove. Ora, dato che nessun
fisico può ragionevolmente sostenere la fondatezza di concetti quali "energia
negativa", e simili, rimane da capire l'origine di tale completa
incomunicabilità tra coloro che usano l'energia come concetto teorico ben
definito, in un contesto di teorie verificabili, e coloro che parlano di
energia in modo vago, mitologico, extra-scientifico. Capita inoltre che, oltre
all'incomunicabilità, vi sia anche malafede; questo avviene quando coloro che
lavorano con i flussi di energia negativa, e quant'altro, rivestono le loro
argomentazioni di una parvenza di scientificità, approfittando della parziale
sovrapposizione dei vocabolari della scienza e della non-scienza. In questo
caso la scienza viene strumentalmente invocata a garanzia di veridicità. Vale
quanto detto sull'energetica di Ostwald: il fruitore di queste conoscenze non
è quasi mai in grado di distinguere criticamente il verosimile
dall'inverosimile, la scienza dalla non-scienza, e si limita ad accettare ciò
che più direttamente sembra rispondere alle sue esigenze (pagandone pure il
prezzo in valuta corrente). E' interessante notare, inoltre, che i concetti
più frequentemente usati dai venditori di panacee magiche e ideologie new-age
sono quelli che prima appartenevano a teorie fisiche confutate, come costumi
teatrali dismessi, non più utilizzabili sul palco ma ancora pieni di lustrini.
Così è per il Magnetismo (quello con la M maiuscola, delle teorie pre-Oersted
e pre-Maxwell), l'Energia (quella di Ostwald), l'etere e il calorico (fluidi
impalpabili come l'aura) e molti altri. Credo che tutto ciò sia in parte
inevitabile ma, tant'è, bisogna pure che chi si occupa di scienza, e chi
insegna scienza, perseveri nel sostenere il valore della razionalità
sull'irrazionalità e della conoscenza sull'ignoranza, anche al prezzo di
qualche delusione. Questo vale a maggior ragione per un insegnante di fisica e
matematica nelle scuole superiori, dove l'esposizione a teorie
pseudo-scientifiche è molto forte. [A parziale giustificazione dell'insistenza
con cui ho trattato quest'ultimo argomento, si consideri che, mentre preparavo
la lezione sull'energia, annotando a fianco del testo alcuni frasi sulle
critiche di Ostwald a Boltzmann, mi trovavo in uno scompartimento di un treno
e, neanche a farlo apposta, una signora, peraltro giovane e intenta a giocare
a scacchi, s'è messa a discutere con un suo amico (l'altro giocatore) riguardo
all'energia negativa che emanava non ricordo da dove...]
Coordinate generalizzate: sono i parametri indipendenti
q1,q2,...,qn che determinano completamente la
configurazione di un sistema meccanico, cioè la posizione di tutti i suoi punti
rispetto ad un dato sistema di riferimento. Per un sistema di punti materiali
liberi si possono prendere semplicemente le coordinate cartesiane x,y,z di
ciascun punto. Il sistema può essere sottoposto a vincoli, in modo che il moto
dei punti sia limitato a un sottospazio dell'usuale spazio tridimensionale (ad
esempio un moto su un piano, su una sfera, ecc.). I vincoli bilaterali
indipendenti dal tempo possono essere espressi tramite un certo numero di
equazioni del tipo
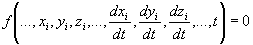 .
.
I vincoli sono detti olonomi se le equazioni che li descrivono
non contengono le derivate rispetto al tempo delle coordinate o possono essere
ridotte in tale forma mediante integrazione. Un sistema meccanico sottoposto a
soli vincoli olonomi è detto sistema olonomo. Per un tale sistema si definiscono
tante coordinate generalizzate quanti sono i gradi di libertà (numero dei
possibili moti indipendenti, compatibili con i vincoli). Ogni variazione
infinitesima della configurazione del sistema, compatibile con i vincoli esterni
all'istante t, è detto spostamento virtuale e può essere scritto nella
forma
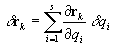 .
.
Allora, il lavoro elementare compiuto durante uno spostamento
virtuale dalle forze che agiscono su un sistema olonomo con s gradi di
libertà vale
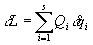 ,
,
dove Qi è detta forza generalizzata. Se i vincoli
sono privi di attrito (o ideali) le forze generalizzate sono fissate unicamente
dalle forze applicate (non vincolari), i vincoli essendo già implicitamente
inclusi tramite le definizioni delle coordinate generalizzate. Se, inoltre, le
forze applicate sono conservative, le forze generalizzate possono essere
espresse tramite l'energia potenziale del sistema
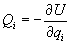 .
.
Funzione di Lagrange: la differenza dell'energia cinetica e
dell'energia potenziale del sistema, espresse in termini delle coordinate
generalizzate, è detta funzione di Lagrange, o lagrangiana. Può essere scritta
come

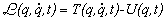 ,
,
dove il punto sopra le variabili indica la derivazione rispetto
al tempo. In questo caso la lettera q indica l'insieme delle coordinate
generalizzate.
Equazione di Lagrange: si può dimostrare, a partire dalle
leggi già enunciate, che il moto di un sistema olonomo soggetto a forze
conservative obbedisce all'equazione
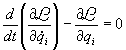 ,
,
detta equazione di Lagrange. Tale equazione può essere
generalizzata al caso di sistemi olonomi qualsiasi, introducendo potenziali
generalizzati e funzioni dissipative. La soluzione dell'equazione di Lagrange
per un dato sistema è equivalente all'uso delle tre leggi di Newton [un' altra
formulazione equivalente consiste nell'introdurre la funzione di Hamilton
(hamiltoniana) e scrivere le equazioni canoniche di Hamilton; ma non discutiamo
qui questo problema].
Princìpi variazionali: le equazioni del moto di un sistema
meccanico o le sue condizioni di equilibrio possono essere ottenute come
risultato di certi procedimenti generali chiamati princìpi variazionali della
meccanica. I princìpi variazionali mostrano in che cosa lo stato reale di un
sistema meccanico differisca da tutti gli altri suoi possibili stati virtuali
compatibili con i vincoli impostigli. Uno di essi è il principio di minima
azione: tra tutti i moti virtuali ammessi per il passaggio di un sistema
meccanico da una configurazione iniziale all'istante ti ad una
configurazione finale all'istante tf (definite da due insiemi
di coordinate generalizzate qi e qf ), il
moto reale del sistema avviene in modo che l' integrale
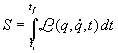
assuma il valore minimo. La funzione S è detta azione.
Il principio di minima azione vale per i sistemi olonomi.
L'introduzione dei princìpi variazionali, in questo punto del
manuale, pone il problema di quali siano veramente i princìpi della meccanica.
Qui viene detto che il problema del moto può essere risolto interamente a
partire dai princìpi variazionali, quale il principio di minima azione. Ma,
per ragioni di sintesi, non viene fornito esplicitamente il legame con gli
altri princìpi precedentemente introdotti (inerzia, azione-reazione, ecc.).
Rimane sottinteso, nel testo, un qualche tipo di equivalenza tra le due
formulazioni, quella che parte delle leggi di Newton e quella che parte dai
princìpi variazionali. In effetti, il principio di minima azione può essere
dimostrato, in senso matematico, dalle leggi di Newton oppure si possono
derivare le leggi di Newton a partire da esso, garantendo alla teoria lo
stessa validità e lo stesso significato fisico (con l'usuale procedura di
validazione tramite osservazioni e misure).
In una manuale sintetico, come quello preso in
considerazione, non c'è spazio per una discussione approfondita di tale
aspetto, ma lo stesso problema si può ritrovare nei testi di insegnamento
universitario (nelle scuole secondarie la meccanica analitica non viene
affrontata). In sostanza, chi studia superficialmente la meccanica può essere
confuso dall'apparente sovrabbondanza di princìpi. La sovrabbondanza di
princìpi si porta appresso il rischio di una interpretazione nominalista della
scienza, ovvero, l' idea che gli scienziati, invece di studiare la realtà, ne
forniscano una rappresentazione fittizia fatta sostanzialmente di definizioni
arbitrarie, pur coerenti tra loro. Per evitare questo rischio, la
presentazione di una teoria dovrebbe rendere evidente, da subito, quali siano
i (pochi) princìpi basilari e, da questi, derivare le conseguenze in termini
di leggi fisiche. Come si capisce da questo manuale, la scelta dei princìpi
non è però univoca.
Integrali del moto e leggi di conservazione: a partire
dall'equazione di Lagrange è possibile discutere , in maniera diretta, il
problema delle quantità conservate. Infatti, le soluzioni dell'equazione di
Lagrange per un sistema meccanico a s gradi di libertà, contengono
2s costanti arbitrarie associate alle posizioni e alle velocità iniziali
dei punti del sistema. Possono allora essere scritte nella forma
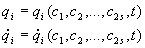
con i=1,2,...,s. Da queste equazioni è possibile
eliminare il tempo e quindi trovare, per ogni sistema meccanico, delle funzioni
delle coordinate e delle velocità generalizzate che restano costanti nel tempo.
Queste funzioni sono dette integrali del moto. La ricerca di tali integrali del
moto è il compito principale della meccanica. Tra questi integrali del moto ve
ne sono alcuni più importanti, la cui costanza nel tempo deriva da proprietà
fondamentali dello spazio e del tempo. Ad esempio, si può facilmente dimostrare
che la conservazione dell'energia totale, E=T+U=costante, è ottenuta
dall'equazione di Lagrange imponendo che la lagrangiana non dipenda
esplicitamente dal tempo (¶ L/¶ t = 0). Ciò equivale a dire che le equazioni del moto non
dipendono dalla scelta dell'origine dei tempi (omogeneità del tempo). L'energia
E è dunque un integrale del moto. In modo analogo si può verificare che
l'equazione di Lagrange implica la conservazione della quantità di moto per un
sistema isolato, qualora si assuma che le proprietà meccaniche di un sistema
isolato non cambino per effetto di una traslazione globale (omogeneità dello
spazio). L'isotropia dello spazio (indipendenza del comportamento meccanico
dalla scelta dell' orientazione degli assi del sistema di riferimento) conduce
infine alla conservazione di un'altra quantità, detta momento angolare, o
momento della quantità di moto. Così, ogni sistema meccanico isolato ammette
almeno sette integrali del moto (sette leggi di conservazione in forma scalare):
una per l'energia, tre per le componenti della quantità di moto e tre per le
componenti del momento angolare.
Siamo dunque arrivati alla conclusione di questa prima serie
di commenti al manuale. Dopo questa analisi, la teoria appare scomposta in
frammenti aventi diversa origine e diverso significato. Il filo logico che li
unisce sembra meno definito di quanto lo era dopo la prima lettura
superficiale. Ma questo non è tanto un problema di questo specifico manuale,
quanto piuttosto una conseguenza della natura stessa della scienza fisica.
Benchè su scala locale il progresso delle conoscenze fisiche
sembri lineare (esperimenti --> ipotesi e definizioni --> leggi -->
nuovi esperimenti --> nuove ipotesi e nuove leggi --> ecc.), se preso
globalmente non è affatto lineare, non procede per accumulo successivo di
definizioni e leggi. Piuttosto, esso è il prodotto di percorsi più o meno
autonomi, più o meno intersecantesi, a cui ogni epoca e ogni scuola
partecipato con il proprio linguaggio e le proprie esigenze.
Lo sforzo di presentare una teoria compiuta, per
l'insegnamento o per la ricerca, consiste anche nel scegliere un filo logico
su cui imbastire un percorso coerente. Così, si può decidere di derivare tutte
le leggi della meccanica classica da un numero limitato di principi
variazionali, come il principio di minima azione, e da alcune assunzioni
generali sulla natura dello spazio-tempo (si veda, per esempio, il primo
volume del corso di Fisica Teorica di Landau e Lifshitz, dedicato alla
meccanica) oppure si può seguire un'impostazione più newtoniana, che ruota
attorno alla definizione di forza e al principio di azione e reazione.
La scelta tra i diversi percorsi è arbitraria, purché non si
perdano di vista i continui e necessari punti di contatto con la verifica
sperimentale. Ma l' arbitrarietà nella formulazione delle teorie non potrebbe
essere sintomo di una mancanza di "verità" nelle leggi fisiche? Dal punto di
vista di un fisico il problema del valore della scienza, implicito in un
domanda del genere, si risolve insistendo sull'importanza dell'osservazione
(intersoggettiva, basata sulla misura). è proprio la possibilità di una
verifica sperimentale che garantisce il valore della conoscenza scientifica al
di là delle arbitrarie scelte linguistiche e formali.
A complemento di questa parte si suggerisce la lettura delle
prime pagine del testo di Laudau e Lifshitz, già citato. Il testo parte dal
formalismo lagrangiano, il principio di minima azione e il principio di
relatività galileiana; prosegue con le leggi di conservazione e, infine, con
le equazioni del moto. è comune, tra i fisici degli ultimi decenni, ritenere
una tale formulazione della meccanica più "elegante". L'eleganza, in questo
contesto, esprime il fatto che i fisici odierni riconoscono in questo tipo di
impostazione alcuni strumenti concettuali efficaci ad affrontare problemi di
fisica moderna, ben al di là della meccanica classica, come la fisica dei
campi, la meccanica quantistica, la teoria della relatività. La meccanica
classica, se espressa in questo linguaggio, emerge come primo passo di una
evoluzione che arriva a comprendere la fisica moderna e, allo stesso tempo,
come caso limite delle teorie più recenti, qualora si facciano ipotesi del
tipo "piccole velocità", rispetto a quella della luce, o corpi "macroscopici",
e così via. Ma questo concetto di eleganza potrà ben cambiare nelle epoche
future quando, inevitabilmente, nuove teorie rimpiazzeranno quelle attualmente
in voga e nuovi linguaggi (matematici e non) saranno utilizzati.
Un manuale qualsiasi corrisponde ad una fotografia dello
stato delle conoscenze; riflette, magari da diverse angolature, un situazione,
un'epoca. Nel passare degli anni la "foto di gruppo" della fisica cambia, si
spostano gli elementi, nascono e muoiono i concetti. Lo stesso testo che ha
dato il via alla meccanica classica, i "Princìpi matematici della filosofia
naturale" di Isaac Newton, costituisce una foto delle conoscenze dell'epoca,
fatta con una veste nuova e con alcune novità concettuali, introdotte
genialmente dallo stesso Newton. Come si passi da quella foto del 1687 all'
immagine odierna della fisica, è un problema che riguarda non soltanto gli
storici della scienza, ma la scienza intera. è l'evoluzione stessa della
conoscenza che ci indica, infatti, quali siano le regole per procedere o, in
altri termini, quale sia il "metodo scientifico".
[ indietro ] [ indice ] [ avanti ]




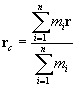 .
.