Finora abbiamo letto un manuale di fisica, lo abbiamo riletto facendone una analisi critica; abbiamo anche detto che si possono scrivere manuali, egualmente corretti, in cui gli stessi contenuti siano presentati in ordine inverso. Complessivamente questo percorso porta ad una scomposizione della fisica in singoli elementi, ciascuno avente una sua storia e un suo significato, non sempre univoco. Ora, volendo arrivare ad una nuova sintesi, conviene abbandonare il manuale e tentare una ricomposizione in qualche modo trasversale, estraendo dall'analisi dei fondamenti della meccanica gli elementi costitutivi del metodo scientifico. Intendiamo cioè partire da domande del tipo:
Ben inteso, qui lo scopo non è tanto quello di dare risposte originali e compiute a tali quesiti (l'autore di questi appunti non essendo né epistemologo né storico della scienza), ma piuttosto quello di raccogliere alcune idee, già parzialmente anticipate nell'analisi precedente oppure raccolte da altri testi, privilegiando aspetti di metodo rispetto a quelli di contenuto.
Prima di procedere però, liberiamoci fin d'ora di un possibile equivoco. Di fronte alla frequente difficoltà di mettere nel giusto ordine le conoscenze acquisite tramite teorie ed esperimenti (ad esempio, per poterle insegnare in modo sintetico e chiaro), si potrebbe essere tentati di dare minor peso ai contenuti delle teorie fisiche a favore del "metodo" accettando, come una sorta di postulato, l'esistenza di quelle regole chiare e, soprattutto, costanti nel tempo che costituiscono, appunto, il "metodo scientifico". In altre parole, se da una parte le teorie sono vaghe meteore che nascono e muoiono secondo una loro specifica e complicata evoluzione, il "metodo" rimane intatto, come struttura portante del lavoro di ricerca e garanzia del progresso complessivo delle conoscenze. Una tale visione, che viene spesso adottata acriticamente, non è tuttavia giustificata. Essa pone il metodo al di fuori o, meglio, al di sopra dei processi storici, dello sviluppo delle singole idee, delle modificazioni del linguaggio e degli strumenti di indagine.
In realtà, le regole che costituiscono il cosiddetto metodo scientifico non possono far altro che partecipare anch'esse, come i contenuti delle teorie, al complesso sviluppo delle conoscenze umane, seguendone l'evoluzione. Chiunque voglia estrarre dalla trama delle ricerche scientifiche un insieme di regole con cui definire un "metodo" indipendente dai contenuti, e privilegiato rispetto a questi, lo potrà fare entro ambiti limitati di fenomeni e di epoche. Un qualsiasi tentativo di estendere questa procedura a tutti i fenomeni indagati dalla scienza e a tutte le epoche (successive a qualche epoca presa, convenzionalmente, come inizio della scienza stessa) incontrerà serie difficoltà. Il risultato dell'operazione finirebbe probabilmente col ridursi ad un insieme di pochi elementi ovvi, come il fatto di considerare conoscenza scientifica solo ciò che è compatibile con le osservazioni, stabilendo delle procedure sensate per quantificare le osservazioni stesse e connetterle tramite un linguaggio matematico. Tutto ciò non è sufficiente a definire un metodo essendo, tuttalpiù, una dichiarazione di intenti, come il primo articolo di una costituzione non è sufficiente a stabilire le regole per governare una nazione. Tutto il resto evolve. In questo senso, l'insieme delle teorie fisiche ritenute valide in una certa epoca non è scindibile dall'insieme delle regole con cui tali teorie sono state ottenute e verificate.
a) Due definizioni di massa
Il libro di Newton, "I princìpi matematici della filosofia naturale", inizia con la seguente definizione "(DEFINIZIONE I): la quantità di materia è la misura della medesima ricavata dal prodotto della sua densità per il volume. Aria di densità doppia, in uno spazio a sua volta doppio, diventa quadrupla; in uno triplice, sestupla. La medesima cosa si capisca per la neve e la polvere condensate per compressione e liquefazione. E la norma di tutti i corpi, che siano diversamente condensati per cause qualsiasi, è identica. In seguito indicherò questa quantità indifferentemente con i nomi di corpo o massa. Tale quantità diviene nota attraverso il peso di ciascun corpo. Per mezzo di esperimenti molto accurati sui pendoli, trovai che è proporzionale al peso, come in seguito mostrerò."
Il testo di meccanica di Landau e Lifshitz, invece, si apre con la definizione della funzione di Lagrange, il principio di minima azione e il principio di relatività galileiano. La massa compare solo quando si introduce la funzione di Lagrange per una particella libera. Se lo spazio e il tempo sono omogenei e lo spazio è pure isotropo, allora la funzione di Lagrange di una particella può dipendere dalla sua velocità solo tramite il quadrato, L(v2). Applicando il principio di relatività galileiana al moto di una particella libera si trova che tale dipendenza può essere solo di proporzionalità diretta. Nella traduzione inglese si trovano le parole: "the Lagrangian is in this case proportional to the square of the velocity, and we write it as L= (1/2) m v2. [...] The quantity m which appears in the Lagrangian is called the mass of the particle." Nella traduzione italiana, invece, si trova scritto: "la funzione di Lagrange nel caso considerato è proporzionale al quadrato della velocità: L=av2. [...] La costante a viene comunemente indicata con m/2". Ho volutamente riportato le due traduzioni per sottolineare l'uso del termine "comunemente", che sottolinea la natura convenzionale della definizione e che, nella traduzione inglese, appare sottintesa. Il testo poi prosegue precisando che l'unità di misura delle massa è arbitraria, dato che, per la proprietà di additività della funzione di Lagrange, la moltiplicazione di tutte le masse di un sistema per una costante arbitraria non modifica la descrizione del moto, fissata unicamente dai rapporti tra le masse delle diverse particelle. Il principio di minima azione, applicato ad una singola particella, stabilisce anche che la massa è una quantità non negativa.
b) Le convenzioni arbitrarie e convenienti
Il confronto tra le due definizioni di massa ci permette di approfondire alcuni aspetti interessanti. Il primo, più banale, è il problema delle convenzioni in senso stretto. Si consideri il fatto che Newton fu il primo ad enunciare definizioni di massa e forza sufficienti a formulare una teoria per la dinamica dei corpi. Era dunque libero di definire tali oggetti nel modo più semplice. La sua massa e la sua forza sono tali che l'equazione del moto appare la più "economica": F=ma. Sviluppando il formalismo newtoniano per includere il concetto di energia, come fatto nel XIX secolo, si trova che l'energia cinetica di una particella libera è (1/2) m v2. Si noti, tuttavia, che anche questo risultato segue in qualche modo da una convenzione: la definizione stessa di energia. Se l'energia cinetica è il lavoro fatto per arrestare un corpo inizialmente in movimento con velocità v e il lavoro è il prodotto di forza e spostamento (più precisamente, l'integrale lungo la traiettoria dei lavori elementari dati dal prodotto scalare della forza per lo spostamento infinitesimo), allora l'energia cinetica è (1/2)mv2. Ma queste definizioni di lavoro e di energia non sono contenute nella formulazione newtoniana della dinamica. La loro introduzione ha ovviamente comportato l'accettazione di convenzioni. Così come era stata definita la quantità di moto come prodotto mv, non si potrebbe definire un'altra grandezza fisica fondamentale come mv2? Potremmo chiamarla vis viva o energia cinetica, associata ad un corpo in movimento. Risulta però più conveniente definire lavoro ed energia in modo che l'energia sia (1/2)mv2 invece di mv2, nel senso che le equazioni che descrivono la conservazione dell'energia, inclusi i processi che coinvolgono flussi di calore, risultano semplici ed efficaci in quel modo.
Vista nell'ottica della dinamica newtoniana, l'introduzione del concetto di energia rappresenta una naturale estensione della teoria, ricca di nuove conseguenze, rimanendo nell'ambito di quella che chiamiamo meccanica classica. Con essa viene a risolversi il lungo dibattito sul calorico (calore come fluido che passa da un corpo all'altro), si precisano i termini e il significato della teoria cinetica dei gas (la cui soluzione rimane tuttavia un grosso problema per i fisici del XIX secolo) e si assesta la meccanica analitica. Tale estensione avviene per continuità rispetto alla formulazione newtoniana, cioè in modo da non modificare precedenti definizioni e princìpi. Così, la massa rimane quella che era nel libro di Newton e appare moltiplicata per 1/2 nell'energia cinetica e, dunque, nella funzione di Lagrange.
Il testo di Landau sintetizza l'esito di un'operazione alquanto diversa, che consiste nel prendere l'insieme delle definizioni, princìpi e leggi della meccanica per darne una riformulazione radicale. Ciò che prima era derivato da alcuni princìpi, ora può essere assunto come principio, e viceversa. Maggior peso viene assegnato a proprietà generali dello spazio e del tempo, al principio di relatività e ai princìpi variazionali. Le leggi del moto vengono estratte di conseguenza.
Ad un certo punto di questa riformulazione appare una costante moltiplicativa nella lagrangiana di una particella in moto. Tale costante viene scritta come m/2, dove m viene identificata con una grandezza detta massa. Qui l'introduzione di un fattore 2, a denominatore, appare ben più arbitraria. Chi ci impedisce, infatti, di scrivere quel termine nella funzione di Lagrange come m anziché m/2? Nulla, se non la convenienza di mantenere la continuità con la formulazione newtoniana. Con il fattore 2 incluso, infatti, le equazioni della dinamica assumeranno la stessa forma delle leggi di Newton, con la stessa definizione di massa.
Si tratta dunque di un problema di convenzioni; chi si trova a definire per la prima volta una grandezza fisica, lo farà nel modo più conveniente, tenuto conto di due esigenze importanti: la necessità di mantenere una qualche continuità con le teorie precedenti e quella di garantire semplicità ed efficacia alle leggi che includono le nuove definizioni.
In definitiva, nell'apprendimento o nell'insegnamento di una teoria, si dove saper distinguere due piani: quello delle convenzioni e quello dei contenuti fisici. La cosa non è sempre ovvia, al punto che un atteggiamento estremo in questa direzione può portare ad identificare l'intera scienza con un complesso coerente di espressioni logico-matematiche convenzionali (convenzionalismo). Questo rischio può essere evitato solo stabilendo in maniera precisa quale sia il rapporto tra i contenuti di una teoria e le osservazioni sperimentali o, in termini equivalenti, tra fatti linguistici (definizioni e asserzioni logico-matematiche) e fatti extra-linguistici (dati sperimentali).
c) Estensioni e riformulazioni di una teoria
Al di là delle questioni evidentemente convenzionali, come ad esempio i fattori moltiplicativi arbitrari, possiamo ancora chiederci se la massa di Newton sia proprio la stessa massa introdotta nella Lagrangiana al modo di Landau.
Ritorniamo al problema dell'estensione della dinamica newtoniana ad includere il concetto di energia. Da quanto detto sopra emergono due procedure distinte, che ben rappresentano una prassi consolidata del metodo scientifico. Quando una teoria non è sufficiente a spiegare nuove osservazioni (in questo caso specifico, le leggi di Newton non bastano a spiegare la natura e il comportamento del calore, nonché il rapporto tra processi meccanici e processi termici), i fisici possono aggiungere all'insieme di definizioni e leggi già accettate nuove definizioni e nuove leggi, compatibili con le precedenti, sulla base di congetture, ipotesi ad hoc e verifiche sperimentali. La nuova teoria dunque sarà una semplice estensione, per continuità, della prima.
Un modo diverso di procedere consiste nel riformulare la teoria di partenza nel suo insieme, non solo aggiungendo qualche nuova ipotesi ad hoc, ma anche rielaborando i concetti fondamentali, sostituendone i princìpi e modificando le definizioni. Una tale riedizione della teoria è utile quando, nella nuova forma, essa fa emergere nuovi aspetti significativi, conseguenze interessanti e inattese oppure, ancora, affinità e legami con le altre teorie.
L'energia, dunque, può rappresentare una ipotesi ad hoc inserita nella meccanica newtoniana, mantenendo lo stesso percorso logico dalle definizioni e dai princìpi originari, oppure può diventare essa stessa la chiave di lettura di tutta la dinamica, una volta passati al formalismo lagrangiano (o hamiltoniano) e derivate da esso le leggi del moto. Nel secondo caso, il passo dalla meccanica classica a quella relativistica (ristretta o generale) e a quella quantistica diventa più breve. La discontinuità con la formulazione newtoniana si giustifica, a posteriori, con la maggiore continuità con la fisica moderna. Per il resto, le diverse formulazioni della meccanica classica, purché coerenti al loro interno e compatibili con le stesse osservazioni sperimentali, rimangono equivalenti.
Così, la massa definita da Newton e la massa nel libro di Landau corrispondono alla stessa grandezza fisica nell'ambito di una stessa teoria, malgrado le diverse formulazioni. Ad esempio, entrambe richiedono l'ipotesi aggiuntiva, e indipendente, di equivalenza tra massa gravitazionale e massa inerziale per poter essere legate correttamente al peso dei corpi. Questa ipotesi aggiuntiva non sarà invece necessaria nella teoria della relatività generale, che parte da diversi presupposti e implica un concetto di massa sostanzialmente diverso. Per questo la teoria della relatività generale non è una estensione per continuità della fisica classica. Ma il passaggio tra l'una e l'altra può sembrare un abisso oppure un semplice gradino a seconda di quale formulazione sia stata scelta per l'una e l'altra teoria.
d) Apparenza e contenuto di una definizione
Rileggendo la definizione data da Newton per la massa non può non saltare all'occhio una evidente circolarità: la quantità di materia (o massa) è data dal prodotto della densità per il volume. Ma la densità non è proprio la massa per unità di volume? Come si può definire la densità in modo autonomo? In effetti, lo stesso Newton si affretta a fare degli esempi, come l'aria, la neve, la polvere, ecc., che ai nostri occhi sembrano insoddisfacenti. D'altra parte, aggiunge subito dopo che la massa è legata al peso, come verificato da lui stesso, e questo permette di procedere operativamente nelle misure.
Tutto ciò appare alquanto confuso e stupisce il fatto che tale confusione sia contenuta nelle prime righe del testo fondamentale della meccanica newtoniana. Ma il nostro stupore nasce principalmente dal fatto che noi abbiamo una formazione ben diversa da quella di Newton e dei suoi contemporanei. è ben vero, infatti, che la massa può essere definita meglio, pur mantenendosi nell'ambito della stessa teoria, ma questo richiede strumenti concettuali non disponibili a Newton, né si può pretendere che egli risolva, al primo tentativo di formulare una teoria dinamica, tutte le possibili ambiguità che i nuovi concetti comportano.
Vale la pena allora sottolineare qual è il vero aspetto qualificante della sua definizione di massa: con essa egli riesce a spogliare i corpi di tutte le qualità estranee alla fisica e, grazie a questo, riesce a costruire una teoria fisica coerente ed efficace. Un concetto primitivo di massa era pur presente prima di Newton, spesso confuso con il peso e sempre mescolato con altre "qualità" dei corpi, frutto del bagaglio filosofico delle epoche precedenti. Il tentativo di separare qualità primarie da qualità secondarie, attuato ad esempio da Galileo, Cartesio e Huygens, trova in Newton la sua realizzazione operativa. Ai fini del comportamento dinamico, poco importano le qualità secondarie dei vari corpi; ciò che conta è un solo parametro, la massa, proprio di tutti i corpi e facilmente quantificabile!
Da questo punto di vista è più facile capire la portata delle prime righe dei Principia e le implicazioni che quel libro hanno avuto nella scienza e nella filosofia. " Un corpo concepito come massa fa pensare ad un corpo la cui materia è qualitativamente indifferente. Il che comportava l'invalidazione dello strumento di studio impiegato fino ad allora e, in pari tempo, la necessità di apprestarne uno nuovo, atto a fornire conoscenze di una materia che si sottrae alle deformazioni della soggettività. Newton, per la prima volta, fornisce una definizione sufficientemente attendibile del concetto, il quale oltre che elemento ordinatore della meccanica (è la prima delle definizioni del moto) diventa anche un mezzo per spogliare i corpi di tutto ciò che non poteva essere ridotto alla fisica-matematica. In tal modo Newton portava a compimento l'operazione di liberazione della fisica da proprietà soggettive e incontrollabili iniziata da Galileo. D'ora in poi i dati sensibili serviranno ad informare dell'esistenza di un oggetto, ma il suo studio dovrà essere lasciato alla risoluzione matematica del corpo stesso." (da A. Pala, Commenti ai Princìpi matematici della filosofia naturale di Newton). Detto questo, il modo usato da Newton per scrivere la definizione stessa è questione che riguarda l'insieme delle conoscenze, degli esperimenti e del linguaggio propri dell'epoca.
e) Il mescolamento improprio di linguaggi e concetti.
A proposito di quest'ultima affermazione, è interessante notare che non mancano, tra le diverse definizioni adottate dai manuali odierni, quelle che fanno esplicito riferimento alla "quantità di materia". Queste definizioni, che trovano parziale giustificazione nel desiderio di fornire un'idea di massa più profonda di una semplice definizione operativa, sono da prendere con cautela.
Intanto, dal punto di vista di un fisico, la nuda definizione operativa è già più che sufficiente per procedere; essa contiene in sé un'intuizione riguardo alla dinamica dei corpi e il senso di tale intuizione viene a precisarsi mano a mano che la teoria mostra tutte le sue implicazioni compatibili con le osservazioni sperimentali.
Se però non ci si accontenta di introdurre la massa con molle e carrelli, allora non basta nemmeno riprendere la definizione di Newton e riformularla superficialmente. Ad esempio, affermare che "la massa è la quantità di materia contenuta in un corpo" è, nello spirito di Newton, una tautologia e, di più, un ribaltamento della logica stessa della definizione newtoniana. Newton vuole associare il comportamento dinamico di un corpo ad un unico parametro indipendente da altre qualità proprie del corpo, ignote o soggettive, mentre l'affermazione in questione sottomette tale parametro alla conoscenza della struttura intima del corpo stesso (quanta materia contiene un corpo?).
Qualcuno può dire però che, a differenza di Newton, noi sappiamo che un corpo è composto di atomi e, questi, di altre particelle elementari di cui si conosce più o meno il numero e la massa. Dunque la massa del corpo è la somma delle masse elementari e questo potrebbe essere il senso della frase "la massa è la quantità di materia". L'unico vantaggio di un tale approccio sarebbe quello di trasferire più in profondità l'idea di massa, rendendo i corpi macroscopici più trasparenti rispetto ad una visione moderna della materia. Ciononostante l'affermazione sarebbe sbagliata. La massa di un corpo non è infatti la somma delle masse delle singole particelle elementari, ma contiene contributi non trascurabili delle cosiddette energie di legame. Le "particelle" della teoria newtoniana sono altra cosa rispetto alle particelle elementari della fisica moderna, per le quali, tra l'altro, la fisica classica risulta inadeguata. Quindi, il tentativo di inserire nella definizione di massa, all'inizio della trattazione della dinamica classica, una qualche idea "moderna" di quantità di materia è generalmente inopportuno e, spesso, sbagliato.
Errori e incongruenze nelle definizioni di grandezze fisiche sono spesso sintomo di un pregiudizio sullo sviluppo storico della scienza. Si pensa cioè che l'introduzione di un nuovo concetto nella fisica sia un evento ben localizzato (il fisico P.Pallino introduce la grandezza X nell'anno NNNN per rendere la teoria A compatibile con le osservazioni B, ecc.) e che ogni concetto, una volta introdotto, non richieda revisioni sostanziali ma, tuttalpiù qualche arricchimento di contenuto a seguito di nuove misure. Così la massa newtoniana è la massa tout court, sia che si parli di orbite celesti che di elettroni e atomi.
Nella realtà, invece, ogni grandezza fisica nasce all'interno di un contesto di teorie, di formalismo matematico e di linguaggio in genere, la cui storia non può essere ridotta ad un accumulo lineare di nuove definizioni. Il contesto in cui opera ciascun fisico può essere identificato con un "dizionario", come fa Bellone (Il mondo di carta), oppure come un "paradigma" della scienza normale, come nella visione di Kuhn (La struttura delle rivoluzioni scientifiche) o in altri modi ancora. Dizionari o paradigmi che siano, sono comunque destinati a mutare nel tempo, per strappi, assestamenti lenti o veloci, espansioni e rovesciamenti. Con essi mutano i significati dei nomi. La massa di Newton non è oggi la stessa di allora, anche se essa compare ancora allo stesso modo nella dinamica dei corpi e nella legge di gravitazione, e lo stesso vale per le forze, i campi, lo spazio e il tempo, ecc. (d'altra parte, come potremmo parlare oggi della massa di un quark utilizzando l'idea di quantità di materia, o densità per volume ...).
Dunque, quando si parla di teorie fisiche o si insegna la fisica, è opportuno sincerarsi che il dizionario usato sia coerente al suo interno e in sintonia col dizionario di chi ascolta. L'evoluzione dei dizionari, o dei paradigmi, è uno degli oggetti primari della storia della scienza.
a) La predizione del comportamento futuro di un sistema
La meccanica ha come obiettivo lo studio del moto dei corpi. Studiare il moto significa estrarre dall'osservazione dei corpi in movimento un insieme di leggi che permettano di predire in modo univoco ciò che avverrà ad un corpi in un tempo successivo, una volta assegnato il suo stato iniziale. Lo stato di un sistema meccanico è completamente specificato se si conoscono le posizioni e le velocità dei punti materiali che lo costituiscono. Le leggi fisiche del moto saranno dunque formulate in termini di equazioni che permettono di calcolare posizioni e velocità in istanti successivi; in breve, se tutte le coordinate q e le velocità (dq/dt) sono date ad un certo istante, anche le accelerazioni (d2q/dt2) si intendono univocamente determinate. Le leggi del moto potranno essere quindi scritte come equazioni differenziali di second'ordine. Questo, in sintesi, è il programma di quella che chiamiamo meccanica classica.
Fu certamente Newton il primo a porre il problema del moto in questi termini. Per dirla con le parole di Poincaré (H. Poincaré, La valeur de la science): "Quale significato attribuivano gli antichi alla Legge? Si identificava per essi con una armonia interna, statica per così dire e immutabile; oppure anche come un modello che la natura si sforzava di imitare. Una legge, per noi, non è più questo, per nulla; è piuttosto una relazione costante tra il fenomeno di oggi e quello di domani; in una parola, è un'equazione differenziale." Questa nuova concezione Newton la derivò essenzialmente dal tentativo, peraltro geniale, di mettere su uno stesso piano il moto degli oggetti celesti, note le leggi di Keplero, e quello dei corpi sulla terra (i pendoli e la caduta dei gravi, secondo le esperienze di Galileo e di altri contemporanei). In quell'ambito la meccanica classica è un eccellente strumento di indagine. Se Newton potesse vedere oggi i tabulati delle orbite dei satelliti artificiali, i calcoli dettagliati per il lancio, le correzioni di rotta, l'incrocio con i pianeti per sfruttarne il campo di gravità e rilanciarsi nello spazio verso altri pianeti o verso una cometa, che nel frattempo sta arrivando secondo una precisa traiettoria, ebbene, se potesse vedere tutto questo sarebbe certo stupito dall'efficacia della sua stessa teoria. Noi stessi ne siamo stupiti. Tuttavia, i fenomeni con cui oggi abbiamo a che fare sono talmente numerosi e riguardano ambiti talmente diversi per scale di tempi, di lunghezze, di velocità, ecc., che dobbiamo anche chiederci se il programma della fisica classica sia veramente adeguato, al di là del caso dei corpi celesti (pochi e sufficientemente distanti tra loro) e degli oggetti macroscopici soggetti a forze facilmente identificabili. Nel fare questo incontriamo subito una serie di problemi non banali come, ad esempio:
Questi problemi hanno tutti a che vedere con il determinismo della fisica classica. Analizzarli con un po' di attenzione, come tenteremo di fare nel seguito, potrebbe evitare di tirare conclusioni affrettate sul significato e sulla validità della teoria.
b) L'errore di misura
Cominciamo dunque dal fatto che ad ogni misura è associato un errore, dovuto alla precisione limitata degli strumenti utilizzati. Ne consegue che lo stato iniziale di un sistema non può essere conosciuto con certezza e, quindi, nemmeno lo stato finale sarà noto con certezza. Ne concludiamo che la meccanica classica non è deterministica? No. Il problema degli errori di misura, implicito nel procedimento di validazione di qualsiasi teoria, non modifica il carattere deterministico della meccanica. Infatti, per la fisica classica l'indeterminazione nella misura delle grandezze fisiche, che caratterizzano lo stato di un sistema, è un fattore esterno alla teoria, legato soltanto all'imperfezione degli strumenti sperimentali. Il miglioramento degli strumenti può permettere, senza ostacoli di principio, un accordo sempre migliore tra i dati sperimentali e la teoria. Se siamo interessati a studiare il moto di un proiettile, faremo una valutazione preliminare di quale sia la precisione richiesta agli strumenti di misura disponibili al fine di ottenere un confronto significativo tra osservazioni e predizioni. Sarà sulla base di ragioni pratiche che stabiliremo se una certa precisione nelle misure è sufficiente o se va migliorata. Una volta eseguita la misura dello stato iniziale (posizione e velocità) con la precisione scelta, i dati di ingresso del calcolo teorico saranno numeri reali, come pure i dati in uscita, questi ultimi essendo univocamente determinati dai primi. Potremmo anche quantificare l'effetto dell'indeterminazione iniziale, inserendo nelle equazioni del moto altri numeri che differiscano dai primi per meno dell'errore ammesso nella misura. I numeri in uscita saranno diversi, ma sempre univocamente fissati dai dati in ingresso. Le implicazioni pratiche, e non ovvie, di una procedura del genere le discuteremo più avanti. In ogni caso, la teoria in sé rimane deterministica per il modo stesso con cui è stata formulata.
c) L'ignoranza delle condizioni iniziali nei sistemi a molte particelle
Tolto di mezzo per il momento un possibile malinteso sul ruolo degli errori di misura, osserviamo ora che la maggior parte dei sistemi fisici che ci circondano sono composti da molti corpi che interagiscono tra loro in modo complicato. Estrapolare da questa ricca fenomenologia alcuni sistemi semplici, come un pianeta attorno ad una stella o un pendolo appeso ad un filo inestensibile, è una procedura standard, adatta alla formulazione di modelli che abbiano validità più generale e che producano, infine, teorie utili. Nel nostro caso specifico, dai casi "modello" (che richiedono tra l'altro una buona dose di intuizione) vengono estratte le equazioni del moto della meccanica classica. Se crediamo che esse descrivano la dinamica di ogni sistema fisico, allora dobbiamo porci il problema di applicarle anche ai sistemi complessi, fatti di molti corpi. In tal caso però, sorge spesso una difficoltà insormontabile: non è possibile, per molti sistemi, la misura delle posizioni e delle velocità di tutti i corpi che lo compongono. Dunque, per essi, le equazioni del moto appaiono inutili, mancando parte dell'informazione necessaria ad estrarne predizioni. Un esempio tipico è quello della dinamica di un gas di atomi racchiuso in un certo volume. Come possiamo pensare di misurare le posizioni e le velocità di tutti gli atomi ad un certo istante? Prima che gli atomi divenissero una realtà unanimemente accettata, un fisico poteva anche ritenere tale domanda un nonsense; infondo, una teoria soddisfacente sul comportamento dei gas poteva ben essere ottenuta per altre vie, basandosi su altri princìpi e su grandezze quali la temperatura, la pressione e così via. Se però vi convincete che il gas è composto di atomi, o lo intuite semplicemente, allora la domanda di prima diventa il nodo principale da superare. La teoria cinetica dei gas, sviluppata alquanto faticosamente nel XIX secolo, ha risolto il problema introducendo nella teoria il concetto di probabilità e il formalismo della statistica. è vero, infatti, che la soluzione delle equazioni del moto per le singole particelle è impraticabile, ma le stesse equazioni possono essere usate per predire il comportamento di quantità "medie". Lo stato "macroscopico" del sistema, quello che effettivamente può essere caratterizzato tramite la misura di grandezze come la temperatura, il volume e la pressione, può corrispondere ad un enorme numero di stati "microscopici", tutti egualmente compatibili con quel macrostato. Non possiamo sapere in quale stato microscopico si trovi il sistema, dato che la misura delle quantità che lo caratterizzano è impraticabile. Possiamo però attribuire a questi stati una certa probabilità e possiamo calcolare medie statistiche (velocità quadratica media, numero medio di urti su una parete, ecc.) da associare alle grandezze macroscopiche misurabili. Così Boltzmann ipotizzò che tutti i microstati associati ad un macrostato fossero equiprobabili, da cui segue che un macrostato si ottiene tanto più facilmente quanto è maggiore il numero di microstati con cui lo si può realizzare. Egli mostrò in questo modo che il macrostato più probabile per un gas (chiuso in un recipiente e isolato) era lo stato di equilibrio (gas immobile, temperatura e pressione costanti e uniformi, ecc.) e che se esso veniva allontanato dall'equilibrio vi faceva poi ritorno spontaneamente. Per Boltzmann gli atomi si comportano come i punti materiali nella meccanica newtoniana e la dinamica dei microstati è deterministica. Tuttavia bisogna pagare un prezzo a causa dell'ignoranza sulle posizioni e le velocità dei singoli atomi e questo prezzo sta nel doversi limitare a quantità medie.
d) La freccia del tempo
Il fatto di introdurre concetti statistici nella dinamica dei sistemi a molte particelle ha una conseguenza importante. Nella teoria degli stati termodinamici si introduce una nuova grandezza, l'entropia, che caratterizza la direzione in cui avvengono i processi spontanei. L'entropia in un sistema chiuso non può mai diminuire; lontano dall'equilibrio non può fare altro che aumentare. Questo è il contenuto della II legge della termodinamica. A differenza della prima legge, che equivale alla conservazione dell'energia nel caso in cui sia incluso il passaggio di calore da un sistema ad un altro, la seconda legge implica l'esistenza di una direzione privilegiata per il tempo; passato e futuro non sono interscambiabili nei processi che implicano variazioni di entropia. L'esistenza di una direzione privilegiata del tempo (la cosiddetta freccia del tempo) è consistente con l'esperienza comune. Un sasso che cade nell'acqua sposta l'acqua intorno a sé, producendo schizzi e onde; ma non s'è mai visto un insieme di onde sferiche convergere verso un sasso e spingerlo fuori dall'acqua, in un processo esattamente invertito rispetto al primo. Ma allora nasce un problema: se crediamo che alla base del comportamento macroscopico vi sia la meccanica classica applicata ad un gran numero di atomi e molecole, allora perché il tempo ha una direzione privilegiata? Infatti, le equazioni del moto della meccanica classica sono simmetriche per inversione temporale. Esse non distinguono passato e futuro! Si provi a cambiare il segno del tempo nelle leggi della dinamica: si otterranno soluzioni egualmente possibili. L'esistenza di una freccia del tempo pone limiti alla validità della meccanica classica? La risposta è no. Il punto chiave è la distinzione tra processi possibili e processi probabili. Le condizioni iniziali, in un sistema complesso quanto si vuole, determinano sempre ciò che accadrà dopo. Così possiamo pensare di predisporre tali condizioni in modo da ottenere un certo processo (il sasso che cade in acqua) o il suo inverso (l'acqua che spinge in alto il sasso). Dal punto di vista della dinamica che determina il moto di ogni componente del sistema, entrambi i processi sono possibili. Il problema è che, se le condizioni iniziali coinvolgono un numero enorme di variabili microscopiche, noi non siamo in grado di preparare il sistema nello stato desiderato; è la natura che decide per noi. L'esperienza ci insegna che la natura preparerà sempre le condizioni iniziali in modo tale da determinare un successivo aumento dell'entropia. Condizioni iniziali che producano una diminuzione dell'entropia sono pure possibili, ma sono talmente improbabili che dovremmo attendere un tempo molto lungo (più della vita dell'universo!) per vederle realizzate. Tale possibilità, in questo senso, è come se non esistesse.
e) I sistemi non lineari e il comportamento caotico
Finora abbiamo discusso l'applicabilità della meccanica classica a sistemi complessi, aventi un numero talmente grande di gradi di libertà da rendere impossibile la determinazione completa del suo stato in un qualsiasi istante, in termini delle posizioni e delle velocità delle singole particelle che lo costituiscono. La teoria rimane deterministica, ma la conoscenza del sistema è limitata a quantità medie. Detto questo, si potrebbe pensare che qualsiasi altro sistema, per il quale invece lo stato meccanico ad un certo istante sia determinabile con grande precisione (diciamo, con un errore trascurabile rispetto ai valori tipici delle grandezze in gioco), dia luogo a predizioni certe e facilmente calcolabili. Purtroppo non è così. Esistono infiniti esempi di sistemi apparentemente semplici, trattabili con equazioni semplici, in cui però è praticamente impossibile predire il comportamento futuro a partire da condizioni iniziali note. Tali sistemi vengono chiamati caotici. Il caos introduce una forma di impredicibilità diversa da quella dei sistemi termodinamici; non è l'ignoranza dello stato iniziale ad impedire la conoscenza dettagliata degli stati successivi, bensì il fatto che fluttuazioni infinitesime nello stato iniziale producono variazioni enormi nel comportamento futuro.
Immaginiamo un pendolo composto da un filo a cui sia appesa una sferetta di ferro; sul piano orizzontale sotto il pendolo disponiamo tre calamite uguali, poste ai vertici di un triangolo equilatero. Se lasciamo andare la sferetta da una posizione qualsiasi, essa oscillerà in maniera irregolare, guidata dalla forza peso e dalle forze magnetiche che la attraggono verso ciascuna delle calamite. A causa degli attriti finirà prima o poi per fermarsi in una delle tre posizioni di equilibrio possibili, al di sopra di una calamita. Ci chiediamo: è possibile predire sopra quale calamita si arresta il pendolo a partire da una posizione iniziale assegnata? La meccanica classica, essendo deterministica, ci farebbe rispondere che sì. D'altra parte il sistema è veramente semplice, sia per costruirlo ed eseguire le verifiche, sia per scriverne le equazioni del moto, trattandosi di un solo corpo in un campo esterno noto. Possiamo quindi immaginare di procedere per tentativi, eseguendo misure dirette oppure calcoli con un buon computer. Ad ogni punto iniziale da cui lasciamo andare la sferetta (con velocità nulla per semplificare le cose) associamo un punto colorato, blu, rosso o verde a seconda che la sfera, partita da quel punto, si fermi su una delle tre calamite. Ripetiamo l'esperimento tante volte in modo da colorare la mappa dei punti iniziali (bidimensionale, dato che la terza coordinata spaziale è eliminata dalla condizione che il filo sia teso e la sua lunghezza fissata). Ragionando semplicisticamente ci aspetteremmo di trovare delle zone di colore ben distinte tra loro e separate da linee altrettanto ben definite. Nella realtà non succede questo; accanto ad alcune zone di colore uniforme si avranno zone ampie di colore non ben definito, in cui i punti colorati si dispongono in striscie e macchie di diverse forme e dimensioni. Ripetendo l'esperimento sempre più in dettaglio, vedremmo che tali striscie e macchie si ripetono su scale sempre più piccole. Accanto a ogni punto verde si troveranno punti blu e rossi, per quanto si ingrandisca la mappa. Questa infinita complessità vanifica, nella pratica, il determinismo delle equazioni. Infatti, sia nell'esperimento che nel calcolo numerico la posizione iniziale P non è determinata con infinita precisione ma è data a meno di un errore, diciamo e. La mappa colorata del pendolo ci dice che, per quanto si tenti di ridurre e, si troveranno sempre stati finali molto diversi, tutti compatibili con una posizione iniziale che disti da P per meno di e. Una predizione certa sul comportamento del sistema sarà dunque impraticabile. Questo è ciò che viene chiamato caos in fisica classica.
Seguendo nel tempo il percorso della sferetta in due casi che differiscono per una piccola fluttuazione nella posizione iniziale, troveremmo che le due traiettorie rimangono vicine per un certo periodo, oscillando sopra una calamita e poi passando ad un'altra e così via, ma da un certo istante in poi si distanziano sempre più. Una delle due traiettorie può saltare su una calamita diversa e da lì seguire un percorso completamente distinto dall'altra. In termini di equazioni del moto, l'origine del fenomeno sta nella non linearità. Un pendolo che segua una legge strettamente lineare (forza direttamente proporzionale allo spostamento rispetto al punto di equilibrio) non mostra alcuna caoticità. Sia la storia che la didattica della fisica sono piene di esempi di sistemi lineari, tanto che si è portati a credere che i sistemi non lineari siano una eccezione. Ma è vero piuttosto il contrario. Anche il pendolo più semplice, quello soggetto alla sola forza di gravità è non lineare, dato che le equazioni lineari si ottengono solo approssimando una funzione trigonometrica, sena o tga, con il suo argomento a. Benché questa approssimazione sia corretta per piccoli angoli, gli effetti dei termini di ordine superiore sono facilmente misurabile (e si potrebbe aprire una discussione interessante sul perché lo stesso Galileo li abbia ignorati pur essendo in gradi di misurarli). Nella realtà i sistemi non lineari sono la regola e i fenomeni caotici sono estremamente frequenti. Un tipico esempio è quello della turbolenza nei fluidi, oppure la dinamica dell'atmosfera, con i suoi modelli di previsione meteorologica.
Una volta appurata l'esistenza di processi caotici, dobbiamo rinunciare a qualsiasi predizione? La risposta, ovviamente è no. Consideriamo un sistema di cui sia noto lo stato iniziale entro un margine di errore e ed esaminiamolo dopo un certo tempo T. Possiamo immaginare tutte le repliche possibili di quel sistema con stati iniziali diversi ma che differiscano da quello assegnato per meno di e. Se il loro stato al tempo T differisce anch'esso per meno di e, allora il sistema è deterministico, non solo perché le leggi che ne descrivono l'evoluzione lo sono, ma anche perché la predizione del comportamento del sistema è realizzabile in pratica, includendo gli errori di misura. Se invece, avendo preparato gli stati iniziali entro una indeterminazione e, troviamo che l'indeterminazione tra gli stati al tempo T è cresciuta (ad esempio, esponenzialmente), allora si dirà che il sistema è caotico. Ora, dato che comunque non ha senso pretendere una precisione infinita nella predizione, si dovrà stabilire quale indeterminazione sia ancora accettabile. A questa corrisponderà un limite superiore al tempo T entro cui ha senso fare la predizione; per tempi più lunghi l'incertezza sullo stato finale crescerà oltre l'atteso e le predizioni perderanno ogni utilità. Questo, ad esempio, è il ragionamento che sta alla base dei comunicati meteo, quando viene detto: "previsioni del tempo valide fino a ...". Ma c'è di più. Supponiamo che i tempi tipici entro cui un sistema fa crescere l'indeterminazione e oltre una qualche soglia ragionevole siano troppo brevi, come ad esempio nell'insorgere di turbolenza in una condotta d'acqua o sotto l'ala di un aereo. Dobbiamo rinunciare ad ogni predizione? No, nemmeno in questo caso. Possiamo ancora fornire delle predizioni, solo che esse saranno di tipo statistico, basate sulla probabilità o improbabilità che un certo evento si verifichi in un certo modo. Potremmo introdurre delle leggi empiriche che descrivono correttamente il comportamento del sistema entro certi limiti, includendo implicitamente l'infinita complessità della dinamica caotica. L'applicabilità della meccanica classica dunque rimane qui un problema "pratico", con tutte le interessanti implicazioni che il caos comporta, ma non di principio. Pensare che essa diventi non deterministica quando applicata ai sistemi complessi e caotici è frutto di un malinteso.
d) L'indeterminazione quantistica
La meccanica classica dunque, per quanto detto finora e per quanto dimostrato dall'esperienza, si rivela un'ottima teoria, capace di fornire predizioni sul comportamento futuro di molti sistemi, date le loro condizioni ad un istante iniziale arbitrario. Nel caso dei sistemi complessi, in cui non sia possibile misurare le posizioni e le velocità di tutte le particelle, le predizioni saranno fornite in termini di probabilità e di quantità medie su insiemi statistici. Anche per i sistemi che mostrano un comportamento caotico, semplici o complessi che siano, si potrà usare il linguaggio probabilistico; oppure si porranno limiti alla scala dei tempi entro cui la predizione può essere data con un certo margine di errore assegnato. Una volta sgombrato il campo da alcuni possibili malintesi riguardo alla validità della teoria, rimane ora da chiarire un punto fondamentale: la meccanica classica è la teoria corretta per tutti i processi dinamici noti?
La risposta è negativa. Al livello attuale di conoscenze, la meccanica classica cessa di essere valida in due domini: nel dominio delle alte velocità, prossime a quelle della luce, e nel dominio microscopico (sul significato da dare al termine "microscopico" parleremo in seguito). Nel primo caso si ricorre ai princìpi della relatività di Einstein, modificando le nozioni di tempo, spazio, energia, massa, ecc. Nel secondo, si introducono i princìpi della meccanica quantistica. Le idee principali di queste due teorie sono generalmente note a chi si occupa anche superficialmente di scienza e una trattazione completa esula dagli scopi di questo corso. Tuttavia, c'è un aspetto centrale della meccanica quantistica che qui vale la pena sottolineare perché connesso a quanto discusso diffusamente sopra: il problema dell'indeterminazione della misura.
Se ci chiediamo, in meccanica classica, a cosa corrisponda la completa caratterizzazione dello stato di un sistema, diremmo che essa equivale a dare le posizioni e le velocità di tutti i punti materiali che lo compongono. Naturalmente nella pratica interverranno errori di misura, ma questi sono in qualche modo esterni alla teoria. Si può ben pensare infatti di migliorare gli strumenti di misura in modo da rendere l'errore trascurabile a tutti i fini pratici. La teoria non fissa limiti a tale procedura. Così si possono determinare con grande precisione, ad esempio, le orbite dei pianeti attorno al sole. Una volta scoperti gli elettroni e i nuclei degli atomi, possiamo anche determinare la traiettoria degli elettroni attorno ai nuclei. Qui la meccanica classica cade, dato che le sue predizioni sono in palese disaccordo con i dati sperimentali. Il motivo principale del fallimento è la pretesa, implicita nel programma della dinamica newtoniana, di fornire istante per istante la posizione e la velocità della particella. La meccanica quantistica, che al contrario è in perfetto accordo con le osservazioni, rinuncia a questa conoscenza, rinuncia all'idea di scrivere leggi orarie, tipo r=r(t), e traiettorie. Anzi, pone questa rinuncia come uno dei suoi princìpi base, il principio di indeterminazione. Supponiamo di voler misurare la posizione e la quantità di moto di una particella ad un dato istante. Il risultato per una coordinata sia ad esempio x , con una indeterminazione Dx, e per la quantità di moto nella stessa direzione sia px con indeterminazione Dpx. Il principio stabilisce che il prodotto delle due indeterminazioni (Dx)(Dpx) non è mai inferiore ad una costante, dell'ordine della costante di Planck. Quindi se si predispone un apparato per misurare con enorme precisione la posizione di un elettrone attorno al nucleo, si otterrà una grande incertezza sulla sua quantità di moto e, dunque, sulla sua velocità, e viceversa. Non si tratta di un problema relativo agli strumenti di misura, ma un limite intrinseco posto dalla teoria. Ciò ha come conseguenza diretta l'impossibilità di caratterizzare lo stato di fisico del sistema tramite le posizioni e le velocità delle particelle che lo costituiscono. Lo stato quantistico viene assegnato tramite una funzione d'onda (funzione complessa di r e t), che può essere interpretata come densità di probabilità. La dinamica non sarà più descritta da equazioni differenziali per i punti materiali, ma bensì da equazioni differenziali per funzioni d'onda. L'elettrone attorno al nucleo non ruota seguendo traiettorie classiche ma "occupa" una funzione d'onda (o un "orbitale"). Quest'ultima contiene la massima informazione ottenibile sulla dinamica della particella. Un qualsiasi esperimento atto a caratterizzare la dinamica di un sistema corrisponde alla determinazione dei valori ammessi per le quantità misurabili, che nel linguaggio della meccanica quantistica sono dette "osservabili". A ciascuna osservabile viene associato, dal punto di vista del formalismo teorico, un "operatore" che agisce sulle funzioni d'onda, in modo che l'esito della misura corrisponde al valor medio dell'operatore applicato alla funzione d'onda che rappresenta lo stato del sistema. Così, l'energia dell'elettrone nell'atomo è il valor medio di un operatore, detto Hamiltoniano (formalmente equivalente alla funzione di Hamilton della meccanica classica), calcolato sull'orbitale occupato dall'elettrone stesso. Il fatto che questa energia assuma valori discreti, cioè sia "quantizzata", sta all'origine del nome meccanica quantistica.
La meccanica quantistica risulta essere una buona teoria non solo per sistemi microscopici, come gli atomi e i nuclei, ma anche per oggetti macroscopici la cui struttura e il cui comportamento sono dominati da processi di tipo quantistico. Si pensi ad esempio alle proprietà dei metalli, dei semiconduttori o dei superconduttori, in cui la dinamica degli elettroni (quantistica, non classica) riveste un ruolo fondamentale. Oggetti enormi, come le stelle di neutroni per citare un caso, possono pure essere dominati da effetti quantistici. Viceversa, anche un fascio di elettroni in un tubo catodico può essere descritto dalle equazioni classiche, malgrado gli elettroni siano generalmente considerati oggetti microscopici. Quindi, quando si dice che la meccanica classica va bene per oggetti macroscopici e deve essere sostituita da quella quantistica per oggetti microscopici, si rischiano seri malintesi. è più corretto dire che la meccanica classica resta valida per tutti i processi in cui gli effetti della quantizzazione delle grandezze fisiche rilevanti siano trascurabili. Che questo avvenga più frequentemente in quei sistemi che noi chiamiamo microscopici non è sufficiente a stabilire una linea di demarcazione sicura tra ambito classico e ambito quantistico con i soli termini "macroscopico" e "microscopico".
Un altro malinteso può nascere attorno al carattere deterministico o indeterministico della teoria. Quando si dice che la meccanica quantistica, a differenza di quella classica, non è deterministica, non si intende dire che essa rinunci a qualsiasi predizione sul comportamento di un sistema a partire dal suo stato iniziale, oppure che fornisca predizioni povere di contenuto. Si tratta piuttosto di intendersi sulla procedura da adottare nel caratterizzare lo stato di un sistema. In particolare l'informazione "massima" che questa procedura ammette non è l'informazione "completa" (in senso classico) sulle coordinate e sulle velocità delle particelle, ma bensì l'insieme dei valori assunti da un certo numero di osservabili, compatibilmente con il principio di indeterminazione. Se un sistema classico viene preparato usando l'informazione massimale sul suo stato, ogni osservabile assumerà un valore ben definito e l'evoluzione successiva sarà completamente determinata. Nel caso quantistico, invece, anche se il sistema viene preparato in uno "stato puro", cioè uno stato caratterizzato da una informazione massimale, non si ha alcuna garanzia sul valore univocamente definito per ogni osservabile; alcune osservabili ammetteranno valori diversi se misurate su esemplari dello stesso sistema preparati nell'identico stato puro. La descrizione degli stati e della loro evoluzione passerà dunque attraverso una interpretazione probabilistica. La meccanica quantistica fornisce le leggi (e le equazioni) utili allo scopo e le sue predizioni sono ampiamente confermate dagli esperimenti. Il fatto che la teoria introduca fin dal principio un contenuto probabilistico ha portato a lunghe discussioni sul suo significato profondo, a letture e riletture del principio di indeterminazione secondo diverse scuole di pensiero. Gran parte di queste discussioni, tuttavia, sembrano nascondere un pregiudizio metafisico contro l'indeterminismo o, meglio, a favore di un determinismo in senso stretto, giustificato dal fatto che gran parte delle nostre esperienze comuni si accordano con il determinismo e la causalità della fisica classica. Il punto di vista di un fisico è ben espresso, in questo caso, dal seguente commento di Born: "Io sono propenso ad abbandonare il determinismo nel mondo degli atomi. Ma questo è un problema filosofico a proposito del quale i soli argomenti fisici non sono decisivi".
 |
|
Questa macchia di colore è l'immagina impressa su una fotocamera digitale da una nube di atomi di sodio confinati in una trappola magnetica a temperature prossime allo zero assoluto (qualche decina di nanokelvin). L'estensione spaziale della nube è prossima al limite inferiore fissato dal principio di indeterminazione. In questo sistema, il concetto di traiettoria dei singoli atomi perde significato e si può invece parlare di "onda di materia". |
Tutto quanto detto precedentemente permette di tirare le somme anche su alcune questioni concernenti il metodo scientifico. Qui non intendo proporre una n-esima versione del metodo. Piuttosto vorrei dare ancora qualche spunto di riflessione e, di seguito, proporre la lettura di poche pagine tratte da G. Toraldo di Francia, "L'indagine del mondo fisico", che riassumono egregiamente alcuni tipi di indagine epistemologica.
a) Una sintesi ragionevole del metodo
Cominciamo da una sintesi ragionevole del metodo scientifico, una qualsiasi. Prendiamo il corso di Fisica Generale di Sivuchin. Nel primo volume troviamo la seguente descrizione.
"Ogni volta che si vuole studiare un insieme di fenomeni
naturali è necessario precisare le leggi e i princìpi fondamentali che
permettono di spiegare fenomeni già noti e prevedere l'esistenza di nuovi. Tale
approccio viene definito metodo dei princìpi fondamentali.
Le leggi o i
princìpi fondamentali non si lasciano dimostrare attraverso ragionamenti logici
e la loro validità viene verificata solo attraverso l'esperienza. L'esperienza
importante non è tanto quella che tende a confermare la giustezza dei princìpi
in se stessi, quanto quella che serve a verificare le conseguenze che ne
derivano. Si potrebbe affermare che i princìpi fondamentali sono
generalizzazioni di fatti sperimentali. Dato che le esperienze non abbracciano
tutte le possibili condizioni di evoluzione di un fenomeno e ogni esperienza è
soggetta ad errori, il metodo sperimentale (che d'altronde è il solo a nostra
disposizione) ci permette di confermare la validità dei princìpi fondamentali
soltanto entro i limiti noti a meno degli errori sperimentali. Non appena si
estende il campo di investigazione dei fenomeni naturali e si migliora la
precisione delle misure, i limiti di validità dei princìpi possono essere
estesi. Può capitare che, oltrepassando limiti noti, certi princìpi fondamentali
cessino di essere validi. Si deve procedere quindi ad una loro generalizzazione
o all'introduzione di altri che possiedano un campo di validità più estesa. I
vecchi princìpi conservano tutto il loro valore nel campo in cui erano stati
definiti. La validità e la potenza del metodo dei princìpi fondamentali consiste
nel fatto che tutti i dati che se ne possono trarre con procedimenti logici o
calcoli matematici sono validi nei limiti in cui i princìpi stabiliti
dall'esperienza sono verificati, con la stessa precisione quindi con cui è stato
eseguito l'esperimento."
b) la fisica è sperimentale?
Certo che sì. è l'esperienza, l'osservazione dei fenomeni, che permette di scegliere le caratteristiche necessarie per passare dal fatto reale al suo modello, alla formulazione di ipotesi e alla derivazione di leggi; ed è ancora l'esperienza che stabilisce la validità delle teorie entro i limiti delle misure. è proprio questo che qualifica la fisica come scienza e che, più in generale, dà valore alla scienza stessa. Tuttavia, una lettura troppo superficiale di questo dato può portare a malintesi.
Un fatto sperimentale, o un insieme di fatti sperimentali, non è sufficiente a determinare il progresso della scienza. C'è un equilibrio tra l'atto sperimentale in senso proprio e l'atto creativo-teorico libero. La scienza ha bisogno di un linguaggio tramite il quale esplicitare i suoi contenuti, essa "esige che le riproduzioni mentali delle esperienze sensibili abbiano forma concettuale" (Mach). Il fatto sperimentale bruto è esterno al linguaggio e non può da solo verificare o contraddire le asserzioni scientifiche. è una illusione empirista quella che vede la scienza come raccolta sensata di informazioni estratte direttamente dalle osservazioni sperimentali. Come se bastasse guardare la luna sufficientemente a lungo per dedurne le leggi di gravitazione. La luna non ci direbbe nulla sulla gravitazione se non esistesse la libera attività concettuale, l'argomentazione logica, l'intuizione, il piacere delle congetture azzardate. Così la scienza ruota attorno ai fatti sperimentali, se ne serve per stimolare ipotesi e per verificarne le conseguenze, ma non si esaurisce con essi.
La natura è ricca e complessa; per comprenderne i meccanismi profondi non basta osservarla. Bisogna dapprima separare due livelli di conoscenza distinti: il perché e il come. Se osserviamo che tutti i corpi tendono a cadere al suolo, possiamo chiederci perché lo fanno e come lo fanno. La fisica procede allo studio del come e a tale fine indirizza i suoi sforzi, stabilendo criteri e metodi per ottenere la massima conoscenza quantitativa dei fenomeni compatibilmente con i limiti delle sue procedure. La fisica non nega dignità al perché dei fenomeni, ma lascia tali questioni alla libera attività intellettuale, sapendo peraltro che l'estensione della conoscenza sul fronte del come aiuta a precisare i limiti e le finalità della ricerca dei perché.
In questo senso si dice che la fisica è nata con Galileo. Egli è infatti il primo a comprendere la centralità di questa distinzione e il senso dell'atto sperimentale. Prima di lui la fisica era confusa con la metafisica. Di fronte al sasso che cade l'aristotelico di turno affermava che esso cadeva perché la terra era il suo luogo naturale. Galileo parte da un diverso presupposto e si chiede soltanto come avviene la caduta. Una conseguenza diretta di questa scelta è un'altra scelta: tra i tanti fenomeni osservabili è necessario scegliere anche cosa è opportuno osservare. Bisogna infatti stabilire un metodo operativo per misurare un fenomeno nelle condizioni migliori possibili, ripetibili, in modo da estrarne numeri, proporzioni, leggi matematiche. Per la caduta dei gravi egli sceglie di sperimentare con pendoli e piani inclinati. Galileo dunque opera il passaggio fondamentale tra osservazione e esperimento, tra esperienza e "sensata esperienza". Non basta stare a sentire la natura che ci parla, ma bisogna interrogarla; è l'uomo che ha il compito di formulare le domande adatte e le dovrà formulare nel modo migliore. Siccome ogni fenomeno dipende da molti fattori (o parametri), formulare la domanda in modo sensato equivale a spogliare ciascun fenomeno dai fattori ritenuti inessenziali o di disturbo e concentrarsi sugli effetti dei fattori ritenuti essenziali. Ciò richiede delle congetture preliminari la cui validità sarà giudicata a posteriori. Si stabilisce così quella simbiosi tra osservazione dei fatti e attività teorica che costituisce l'essenza stessa del progresso scientifico.
c) il principio di continuità e l'immaginazione
Sarebbe ben difficile formulare teorie di validità generale, applicabili ad ampie classi di fenomeni, senza un principio di continuità. Una volta selezionato e studiato un caso particolare e formulata una idea su di esso, il principio di continuità consiste nell'applicazione della stessa idea ai casi che differiscono da quello dato per variazioni graduali, come ad esempio la variazione continua di uno dei parametri in gioco. Fu ancora Galileo a capire la portata di tale metodo. Basti pensare alla sua derivazione della legge d'inerzia. Una sfera che scende da un piano inclinato e risale lungo un secondo piano, viene rallentata progressivamente da quest'ultimo. Il rallentamento dipende dall'inclinazione in modo che, quando questa viene gradualmente ridotta, esso diventa mano a mano minore. Per continuità, se il secondo piano avesse inclinazione nulla il rallentamento stesso sarebbe nullo e la sfera proseguirebbe a velocità uniforme.
Un altro caso ancora più significativo è quello della legge di gravitazione newtoniana. Newton ha modo di osservare, come tutti i suoi predecessori, i moti governati dalla gravità sulla terra e la rotazione della luna attorno alla terra. Egli intuisce che tra questi due fenomeni vi sia una parentela, un relazione di continuità. Come fisico postgalileiano è abituato a ragionare secondo un principio di continuità. Anche contro le apparenze è disposto ad assumere che le proprietà della natura in un certo luogo e in un certo istante siano le stesse ovunque e sempre, salvo verificarne poi le conseguenze. "Il fisico abituato alla continuità dei pensieri, poiché constata la presenza dell'attrazione gravitazionale non solo sulla superficie della terra, ma anche in cima alle montagne e in fondo alle miniere, immagina che quest'attrazione agisca ad altezze e profondità per lui inaccessibili. Egli si chiede: dov'è il limite per l'azione della gravità terrestre? Non si estenderà per caso fino alla luna?" (Mach).
Newton non ha mai verificato sperimentalmente che la legge di gravità è valida in tutto lo spazio tra sé e la luna; ha semplicemente proiettato l'idea di gravità lontano dal suo luogo d'origine e su queste basi ha fondato la gravitazione universale.
Il principio di continuità non deriva dalla natura delle procedure sperimentali, ma né è autonomo, essendo piuttosto uno strumento per gli atti speculativi, una prassi del pensiero, un modo per rendere efficace l'immaginazione. In questo senso, sarebbe fortemente limitativo affermare che la legge di gravitazione, come tante altre leggi fisiche, è il frutto di esperimenti. Quando si dice che la fisica è una scienza sperimentale non si intende che i suoi progressi siano riconducibili a puri atti sperimentali, ma piuttosto che ogni speculazione, ogni congettura, ogni frutto dell'intuizione e dell'immaginazione deve passare al vaglio delle misure.
d) la valutazione estetica e il rapporto con la matematica
Questo nostro tentativo di spogliare il discorso sul metodo scientifico dai possibili malintesi di una lettura superficiale non è ancora terminato. Ci preme ancora sottolineare l'apertura del metodo ad elementi apparentemente estranei ad esso e la potenziale ricchezza che questo comporta. E questo lo facciamo per equilibrare una tendenza contraria, quella cioè di ritenere che la scienza è tanto più corretta ed affidabile, quanto meglio sono delimitate e definite le regole che ne costituiscono il metodo. Tale tendenza è giustificata dalla sacrosanta necessità di marcare la distinzione tra la scienza e altre nobili attività (filosofia, religione, politica, ecc.) ed anche, forse con maggior preoccupazione, per salvaguardare la scienza stessa dalle dottrine pseudo-scientifiche o anti-scientifiche che popolano l'universo del pensiero umano.
Tuttavia, ogni volta che si tenta di racchiudere il metodo scientifico in un insieme limitato di regole, si finisce per lasciare fuori dalla porta elementi utili, a volte anche essenziali. Un caso già citato precedentemente è quello di Ernst Mach. Questi formulò una teoria fenomenistica della scienza, in cui le teorie fisiche risultano essere descrizioni approssimative e imprecise dei fenomeni reali, derivate secondo regole ben definite e secondo criteri di economicità, ossia riducendo al minimo il dispendio di pensiero. Applicando rigorosamente questo schema, Mach giunge tra l'altro a considerare la teoria atomica come un espediente matematico provvisorio, atto a rappresentare in modo più o meno impreciso la realtà, ma nega l'esistenza reale degli atomi. Finisce dunque per essere vittima del suo stesso pregiudizio metodologico, mentre altri suoi contemporanei aprivano la strada alla moderna fisica atomica.
Come esempio concreto di elemento apparentemente estraneo alla fisica, consideriamo il caso del giudizio estetico. Riteniamo che esso sia rilevante nella formulazione di leggi fisiche? La risposta non è scontata. Consideriamo due possibili punti di vista estremi. Da una parte si può affermare che il giudizio estetico appartiene alla sfera delle sensazioni soggettive e che non vi è ragione di credere che esso vincoli il comportamento della natura, in quanto realtà oggettiva. La natura fa quel che fa indipendentemente dalle valutazioni soggettive che i fisici associano alle leggi fisiche, la loro presunta eleganza. Dunque, forzare le teorie ad essere "eleganti" è generalmente sbagliato, essendo una indebita applicazioni di pregiudizi estranei al fatto scientifico. Sul fronte opposto si può invece pensare che la struttura stessa del pensiero umano sia condizionata a priori dal comportamento della natura, così che ciò che ci sembra soggettivamente bello ed elegante rispecchia una intima coerenza con la realtà oggettiva. è la natura stessa che ci suggerisce ciò che è bello. L'applicazione di un giudizio estetico quindi è una naturale conseguenza di un condizionamento esterno che porta a adeguare l'atto soggettivo al fatto oggettivo.
Una valutazione approfondita del significato di queste due impostazioni richiede una analisi dettagliata degli aspetti epistemologici connessi all'oggettività della realtà fisica e della sua rappresentazione in termini di teorie. Qui ci limitiamo a due considerazioni.
La prima, breve, riguarda il fatto che la fisica è sperimentale. Quindi, si può ben dare importanza alla valutazione estetica nello sviluppo di una teoria, ma non si può in alcun modo usarla come criterio di validazione della teoria stessa. Solo il dato sperimentale può garantire la validità o meno delle leggi fisiche. Ciò stabilisce un confine chiaro entro cui è lecito l'utilizzo di criteri di eleganza, simmetria, ecc., senza peraltro entrare nel merito della loro utilità o inutilità.
La seconda considerazione è necessariamente più articolata e riguarda il rapporto tra matematica e fisica. Quando applichiamo un giudizio estetico ad una teoria fisica, in realtà lo applichiamo soprattutto alle equazioni matematiche che esprimono le leggi fisiche e all'insieme di deduzioni e dimostrazioni matematiche che permettono la formulazione della teoria. La matematica obbedisce a regole logico formali a cui si possono applicare valutazioni estetiche senza riferimento a realtà esterne ad essa. Si può dire di più: nello sviluppo della matematica l'estetica è uno degli elementi portanti.
Un punto di vista interessante in proposito è quello del fisico-matematico H.Poincaré (La valeur de la science, 1905): "I matematici hanno un triplice scopo. Essi devono fornire uno strumento per lo studio della natura. Ma non solo: essi hanno anche uno scopo filosofico e, oserei dire, uno scopo estetico. Essi devono aiutare la filosofia a approfondire le nozioni di numero, spazio, tempo. E soprattutto i loro adepti vi trovano un piacere analogo a quello che dà la pittura o la musica. Essi ammirano la delicata armonia dei numeri e delle forme; si meravigliano quando una nuova scoperta apre una prospettiva inattesa; e la gioia che essi provano non ha forse un carattere estetico, anche se i sensi non ne prendono parte? Pochi privilegiati sono chiamati a gustarne il piacere pienamente, questo è vero, ma non è forse questo che accade a tutte le arti più nobili? Per questo non esito a dire che la matematica merita d'essere coltivata per essa stessa e che le teorie che non possono essere applicate alla fisica lo devono essere come le altre. Forse lo scopo della fisica e lo scopo estetico non saranno sempre solidali, ma non dobbiamo sacrificare né l'uno né l'altro. I matematici non dovrebbero essere per i fisici dei puri fornitori di formule; è necessario che la collaborazione reciproca sia più intima."
Un esempio particolarmente convincente di come le valutazioni
estetiche proprie della matematica possano influire positivamente nello sviluppo
di teorie fisiche corrette è quello, già accennato precedentemente nel corso,
delle equazioni di Maxwell per l'elettromagnetismo:
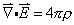
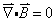
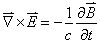
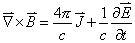
Maxwell si accorse che le leggi fino ad allora note sui fenomeni elettrici e magnetici, e compatibili con tutte gli esperimenti fino ad allora eseguiti, assumevano una forma compatta ed elegante se scritte in termini di campi elettrici e magnetici propriamente definiti. Egli però non si fermò ad una semplice riformulazione di cose note. Una volta scritte le equazioni differenziali per i campi appariva anche evidente una piccola mancanza di simmetria: le equazioni in assenza di cariche e correnti avevano una forma diversa per il campo magnetico e quello elettrico. Maxwell si accorse che bastava aggiungere un termine in più in una delle due equazioni per ricomporre la simmetria. Nessuna osservazione, nessun esperimento glielo suggeriva, ma solo un'esigenza di simmetria. L'aggiunta di quel termine (la cosiddetta corrente di spostamento) produceva effetti talmente piccoli nel contesto degli esperimenti già eseguiti in passato che poteva essere compatibile con questi. Ma esso introduceva anche nuove soluzioni, corrispondenti alla propagazione di onde. Ci vollero vent'anni per avere la prima evidenza sperimentale delle onde elettromagnetiche previste da Maxwell e l'impatto della sua teoria divenne enorme. Dunque per l'introduzione della corrente di spostamento, il movente di Maxwell fu estetico e solo più tardi l'esperimento confermò la validità di quella congettura.
Naturalmente l'introduzione di nuovi elementi di conoscenza non funziona sempre così. In molti casi una legge fisica nasce da una congettura estratta più direttamente dai dati empirici. Abbiamo voluto sottolineare che il metodo scientifico non si identifica necessariamente con quest'ultima modalità.
e) Keplero e l'armonia
 Uno dei
capisaldi su cui poggia la fisica è costituito dalle tre leggi di Keplero per il
moto dei pianeti. La prima dice che i pianeti percorrono orbite ellittiche di
cui il sole occupa uno dei due fuochi; la seconda, che un raggio vettore spazza
aree uguali in tempi uguali. Infine la terza afferma che il rapporto tra il
quadrato del periodo di rivoluzione e il cubo del raggio medio dell'orbita è
costante. Keplero arrivò a tali leggi a partire da certe congetture e tramite il
confronto continuo con i dati astronomici forniti da Tycho Brahe. L'importanza
delle leggi di Keplero deriva anche dal fatto che Newton ne diede una
derivazione matematica sulla base di una nuova e potente teoria dinamica e
sull'idea di gravitazione universale.
Uno dei
capisaldi su cui poggia la fisica è costituito dalle tre leggi di Keplero per il
moto dei pianeti. La prima dice che i pianeti percorrono orbite ellittiche di
cui il sole occupa uno dei due fuochi; la seconda, che un raggio vettore spazza
aree uguali in tempi uguali. Infine la terza afferma che il rapporto tra il
quadrato del periodo di rivoluzione e il cubo del raggio medio dell'orbita è
costante. Keplero arrivò a tali leggi a partire da certe congetture e tramite il
confronto continuo con i dati astronomici forniti da Tycho Brahe. L'importanza
delle leggi di Keplero deriva anche dal fatto che Newton ne diede una
derivazione matematica sulla base di una nuova e potente teoria dinamica e
sull'idea di gravitazione universale.
Abbiamo tutti gli elementi tipici del procedimento scientifico: a) le misure accurate, b) le congetture e le leggi empiriche per l'interpretazione delle misure, c) la formulazione di una teoria generale che spiega i fenomeni e che contiene le leggi empiriche come implicazione diretta di princìpi fondamentali. Un buon libro di testo sulla meccanica non mancherà di far risaltare questa connessione metodologica tra i vari elementi del processo conoscitivo.
Di nuovo, una lettura superficiale potrebbe nascondere delle trappole. L'obiezione maggiore sta nel fatto che sì, Tycho Brahe era un buon sperimentatore, anche in senso moderno, e Newton era un buon fisico, pure in senso moderno, ma Keplero sembra ben lungi dall'applicare un metodo scientifico ai suoi studi astronomici. Insomma Keplero non era un fisico moderno. Un argomento in questa direzione è il modo in cui arrivò alla formulazione della terza legge. Intanto si noti che questa non venne pubblicata assieme alle altre due in un libro di astronomia (Astronomia Nova), ma separatamente in un libro anomalo, intitolato Harmonice Mundi, dedicato ai pianeti, alla musica e all'astrologia. A parte l'astrologia, che per Keplero era fonte di guadagno ma non d'ispirazione, più interessante è la connessione con la musica. Infatti, la terza legge stabilisce che i rapporti dei periodi di rotazioni sono uguali ai rapporti tra i raggi dell'orbita elevati alla potenza 3/2. Ora, il rapporto 3:2 in musica equivale al cosiddetto intervallo sesquialtero (di quinta, nel linguaggio moderno), che è l'intervallo più importante dell'armonia musicale. Ebbene, Keplero si occupava direttamente di studi armonici e il libro Harmonice Mundi è essenzialmente dedicato agli intervalli musicali. Nell'ambito di questi studi Keplero ebbe l'intuizione che anche i pianeti dovessero seguire le leggi dell'armonia e, in base a questa intuizione, verificò che i rapporti tra periodi e raggi erano legati da proporzioni sesquialtere. La terza legge, dunque, rendeva evidente che la musica e il sistema solare erano manifestazioni delle stesse leggi armoniche. Ciò gli bastò anche per ritenere migliore il sistema copernicano rispetto a quello tolemaico, dato che quest'ultimo non permetteva una tale concordanza.
Quindi Keplero giunse a leggi empiriche che tutt'oggi riteniamo corrette, ma vi giunse tramite elementi estranei a quello che noi chiamiamo metodo scientifico, come le analogie tra intervalli musicali e orbite planetarie e vari pregiudizi metafisici sull'armonia dell'universo. Per questo motivo si è riluttanti, oggi, a considerare Keplero come un fisico moderno.
Ma resta un problema di fondo: dato che le leggi di Keplero rappresentano un passo fondamentale nello sviluppo della fisica, possiamo ridurre la loro derivazione originaria e anomala ad un semplice accidente storico? O, in altri termini, possiamo immaginare di sostituire il Keplero reale con un Keplero fittizio, capace di derivare la terza legge dai dati empirici secondo procedure rigorose e senza riferimenti extra-scientifici? Dopo tutto, è questo che si fa quando si forza la lettura storica secondo gli schemi classici esperimento-ipotesi-teoria. Mark Twain diceva: "Nella vita reale la cosa giusta non accade mai al posto giusto e al momento giusto: è compito dello storico rimediare a questo errore". Parafrasando quest'idea, si potrebbe dire che la rimozione dell'elemento extra-scientifico nella derivazione delle leggi di Keplero, operata a posteriori da chi riassume e semplifica lo sviluppo della scienza, tranquillizza chi crede nell'esistenza di un metodo scientifico stabile e ben definito, ma non evita affatto di pensare che simili anomalie siano, in qualche modo, un fatto ricorrente e ancora attuale. Come giudicare, d'altra parte, l'ostinazione con cui molti fisici odierni cercano la "grande unificazione" e le teorie "super-simmetriche"? Dobbiamo pensare che siano mossi da pregiudizi extra-scientifici?
Il punto è un altro. Il confine tra scienza e non scienza va ricercato altrove, non nei mille possibili modi con cui un'idea o una congettura può mettere in moto il processo conoscitivo, ma nelle regole seguite da là in poi. Un giocatore di scacchi può scegliere la prima mossa da fare seguendo le motivazioni e le ispirazioni più diverse, ma ciò che rende possibile riconoscere la partita, in quanto partita a scacchi, e portarla a termine, è l'insieme delle regole entro cui le mosse successive si sviluppano. Nel nostro caso, analogamente, ciò che rende possibile riconoscere la scienza in quanto tale e distinguerla dalla non scienza è l'insieme delle regole adottate per validare o falsificare le conseguenze delle congetture iniziali, sulla base del confronto con le osservazioni empiriche.
Lo stesso Keplero, d'altra parte, era consapevole dell'importanza del "metodo" accanto ai "contenuti", come quando, riferendosi ai modelli astronomici degli antichi, scriveva: "I modi in cui gli uomini giunsero alla conoscenza delle cose celesti mi sembrano quasi tanto meravigliosi quanto la natura stessa di quelle cose". Se questa sua consapevolezza oggi ci pare, non del tutto a ragione, meno moderna, è solo perché vogliamo leggere Keplero usando il nostro linguaggio e non il suo. Ma per tracciare correttamente il cammino della scienza, lo sforzo di traduzione tra un dizionario e l'altro va fatto. E rileggendo Keplero nell'ottica della cultura dell'epoca, dei "paradigmi" operanti allora, dei "dizionari" usati dagli scienziati rinascimentali, si possono dipanare le linee di sviluppo del pensiero, che vanno dalla scuola Pitagorica (armonia e numeri) di 2000 anni prima, fino alle simmetrie della fisica contemporanea. Lo stesso si può fare seguendo altre linee e collegando altri nomi e altri periodi.
Non si tratta di una procedura semplice. Ma perché dovremmo rinunciarci in partenza? Perché dovremmo accettare passivamente visioni eccessivamente riduttive e semplicistiche? Riconoscere la complessità della scienza, e tentare di leggere in profondità il cammino delle sue idee portanti, implica coglierne l'immensa ricchezza, la ricchezza della natura e la ricchezza del rapporto tra l'uomo e la natura.