|
La termodinamica: dal macroscopico al microscopico
|



|
Fatti rilevanti ed altri indizi
1. Una possibile ricostruzione dei fatti
Ovvero, quello che di solito si racconta nei corsi di fisica,
quando si parla della nascita della fisica moderna...
|
Radiazione di corpo nero
Una cavità, le cui pareti sono ad una temperatura costante T
e che abbia un forellino da cui possa entrare o uscire radiazione
elettromagnetica, costituisce quello che i fisici chiamano un
"corpo nero". Il termine deriva dal fatto che la radiazione che
entra nella cavità passando dal foro ha una probabilità
trascurabile di uscirne, così che il foro stesso si
comporta come una superficie perfettamente assorbente (e infatti
appare nero a chi lo guarda dall'esterno). Ad una data temperatura
T le pareti della cavità assorbono ed emettono radiazione
elettromagnetica; all'equilibrio questa riempirà la cavità,
e ad essa sarà associata una certa densità di energia.
Ora, i fisici della fine dell'800 sapevano che la radiazione emessa
dal foro (il potere emissivo) in queste condizioni è esprimibile
in termini della densità di energia della radiazione
nella cavità
ed è una funzione universale della temperatura, nel senso che
non dipende dal tipo di cavità usata. La predizione di questa
funzione universale era uno dei problemi principali che la fisica classica
non era in grado di risolvere.
Il campo
elettro-magnetico nella cavità segue le leggi di Maxwell.
E' rappresentabile da un insieme di oscillatori. Il numero di
oscillatori di frequenza assegnata e per unità di volume
può essere calcolato. Basta assumere che gli
oscillatori che contribuiscono all'energia nella cavità, in
condizioni di equilibrio termico con le pareti a temperatura T,
siano i modi normali della cavità stessa, cioè
quelli tali da sommarsi in fase nelle riflessioni con le pareti.
La densità di modi normali così
calcolata può essere moltiplicata per l'energia media
di ciascun oscillatore. La meccanica statistica classica fornisce
il risultato: ogni oscillatore ha un'energia media pari a kT, dove
k è la costante di Boltzmann (principio di equipartizione).
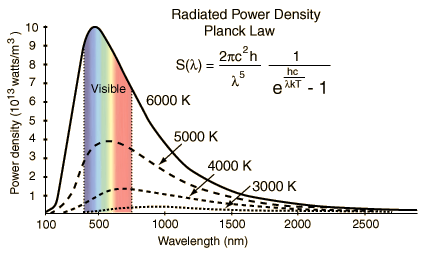
In questo modo si ottiene la legge di Rayleigh-Jeans, secondo cui
la densità di energia della radiazione è proporzionale
a kT e al quadrato della frequenza. Questa legge
non è compatibile con la curva sperimentale. E' buona
solo a basse frequenze, mentre ad alte frequenze predice una
densià di energia che diverge all'infinito, mentre quella
osservata tende esponenzialmente a zero.
Nel 1900 Planck
propose una formula empirica che riproduceva i
dati sperimentali, al prezzo di introdurre una nuova costante
universale h. Si accorse poi che la stessa formula poteva
essere ottenuta utilizzando le leggi statistiche per il calcolo
dell'entropia degli oscillatori e aggiungendo l'ipotesi che
i valori di energia ammessi da ciascun oscillatore non
costituissero un continuo, da zero ad infinito, ma un insieme
discreto di "quanti", ciascun "quanto" essendo il prodotto della
frequenza per una costante universale h, poi chiamata costante di
Planck. Questa ipotesi era ingiustificata da un punto di vista
classico, ma dava predizioni in ottimo accordo con gli
esperimenti. Si poneva quindi il problema di
inquadrare la quantizzazione dell'energia in un contesto di leggi
nuove.
 Effetto fotoelettrico
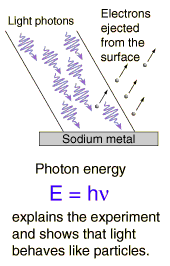
Effetto fotoelettrico
Si tratta di un altro fenomeno per il quale la predizione classica
è incompatibile con le osservazioni.
Una superficie irraggiata da luce emette elettroni.
Con un opportuno apparato si può misurare la corrente prodotta
da tali elettroni in funzione della frequenza e dell'intensità
della luce. Le misure sono incompatibili con la visione classica
di un'onda elettromagnetica che deposita energia sulla superficie
fino a fornire agli elettroni energia sufficiente a liberarli
nel vuoto. Einstein, partendo dall'idea di Planck sulla quantizzazione
dell'energia del campo elettromagnetico, ipotizzò che il processo di
emissione avvenisse tramite urti tra singoli "quanti" di radiazione
e singoli elettroni. Si spiega così: 1) il
fatto che il processo di emissione è istantaneo (non occorre
un tempo di "accumulazione dell'energia sulla superficie", basta che
un singolo quanto arrivi su un elettrone); 2) il fatto che esiste
una frequenza di soglia al di sotto della quale gli elettroni non
vengono emessi (quando l'energia del quanto di radiazione, proporzionale
alla frequenza, è minore del potenziale di estrazione, che
dipende dal tipo di superficie); 3) il fatto che
l'energia con cui vengono emessi gli elettroni non dipenda
dall'intensità ma solo dalla sua frequenza (essendo questa
energia pari alla differenza tra l'energia del quanto di radiazione e il
lavoro di estrazione); 4) il fatto che la corrente indotta nel
circuito è proporzionale all'intensità
della luce (a maggior numero di "quanti" incidenti corrisponde maggior
numero di elettroni emessi). Sulla base del modello di Einstein si
può misurare la costante di Planck usando l'energia degli
elettroni emessi in funzione della frequenza della luce. Ulteriori
misure confermarono questa ipotesi.
Da un punto di vista concettuale il passaggio dalla legge di Planck
per il corpo nero all'ipotesi di Einstein sull'effetto fotoelettrico,
equivale a considerare l'esistenza di quanti di energia come una
proprietà intrinseca della radiazione e non un accidente
associato puramente all'emissione e assorbimento di radiazione da
parte degli atomi. Nella visione di Einstein (sfruttando la teoria
della relatività speciale, appena formulata indipendentemente)
il quanto di energia del campo elettromagnetico
si configura come una possibile
particella di massa a riposo nulla, essendo E=cp la relazione tra
energia e momento. Si tratterà poi di rendere questa
rappresentazione corpuscolare della luce compatibile con quella
ondulatoria, quest'ultima essendo valida per altri fenomeni. Nasce
così un problema relativo al "dualismo onda-particella".
 Calore specifico dei solidi
Calore specifico dei solidi
Un'altro problema aperto all'inizio del '900 era quello del calore
specifico dei solidi. Da un punto di vista classico l'energia
interna di un solido può essere vista come l'energia
associata a 3N oscillatori, corrispondenti ai gradi di libertà
di vibrazione degli atomi attorno alle posizioni di equilibrio
nei siti reticolari. Il principio di equipartizione fissa in kT
l'energia media per ciascun oscillatore. Questo significa un'energia
interna pari a 3NkT e un calore specifico costante pari a 3Nk. Le
misure effettuate su diversi solidi e in funzione di T mostrano
invece che il calore specifico raggiunge 3Nk solo a temperature
maggiori di una certa temperatura tipica, dipendente dal tipo
di solido considerato, mentre al di sotto di questa il suo valore
è minore della predizione classica, tendendo a zero nel
limite T=0. Einstein (nella foto assieme a Bohr)
propose di trattare le vibrazioni degli
atomi come oscillatori soggetti alla stessa regola di quantizzazione
dell'energia della radiazione nel corpo nero. L'energia media
di ciascun oscillatore è minore di kT secondo la formula
di Planck. Non potendo fare un calcolo esatto della densità
di oscillatori (dato che occorrerebbe un modello dettagliato del
solido), Einstein fece la semplice ipotesi che tutti gli atomi
vibrassero indipendentemente con la stessa frequenza. In questo
caso, l'energia interna del solido è semplicemente 3N
volte l'energia media di un oscillatore, ciascuno di essi
avendo energia quantizzata. In
questo modo Einstein trovò un calore specifico che
ha il limite corretto classico ad alte T e che tende a zero
esponenzialmente a basse T.
Dal punto di vista concettuale, l'innovazione maggiore in questo
caso sta nell'aver esteso l'idea di quantizzazione dell'energia
anche al moto di particelle con massa (atomi e molecole). Quindi
la quantizzazione non è propria soltanto del campo
elettromagnetico!!
Spettri atomici e modello di Bohr
Alla fine dell'800 si stavano compiendo esperimenti importanti
riguardanti la struttura della materia (raggi catodici, raggi
canale, radioattività, diffusione di elettroni, diffusione
di raggi alpha...). Ne emergeva un'idea "atomica" della materia,
con gli atomi costituiti da un nucleo positivo di dimensioni
piccolissime, circondato da elettroni che si muovono entro una
regione di raggio dell'ordine di 10^(-10) m.
I primi modelli di atomo si confrontavano con due problemi
principali:
- La stabilità degli atomi. Gli elettroni che si muovono
su orbite classiche attorno al nucleo positivo dovrebbero
emettere radiazione elettromagnetica,
essendo soggetti ad accelerazione, e
quindi perdere energia fino a cadere nel nucleo.
- Lo spettro a righe. Gli elettroni dovrebbero essere in grado
di emettere e assorbire onde e.m. a qualsiasi frequenza, modificando
le loro orbite. Invece, gli spettri osservati presentano righe
discrete. La struttura delle righe nello spettro è particolarmente
semplice nel caso dell'idrogeno, dove è facile individuare delle
"serie spettrali" caratterizzate da leggi empiriche semplici, la
cui natura è incomprensibile dal punto di vista della fisica
classica.
Nel 1913 Bohr propone un modello per l'atomo di idrogeno basato su
due ipotesi principali:
- Gli elettroni non possono muoversi su orbite qualsiasi, ma
stanno solo su orbite circolari "stazionarie" individuate dalla
condizione che il momento angolare dell'elettrone sia un multiplo
intero della costante di Planck divisa per 2 pigreco. Su queste orbite
gli elettroni non emettono radiazione e.m.
- L'emissione e l'assorbimento di radiazione e.m. è
possibile solo tramite transizione di un elettrone da un'orbita
stazionaria ad un'altra; in questo caso, l'assorbimento o
l'emissione avviene per quanti di energia, in modo che
la frequenza della radiazione emessa o assorbita è fissata
dalla differenza di energia tra i due livelli fra cui l'elettrone
transisce.
Con queste ipotesi si spiega lo spettro a righe osservato per
gli atomi di idrogeno (serie di Lyman, di Balmer, di Paschen, ecc.,
oltre al valore della costante di Rydberg). Si tratta di ipotesi
incompatibili con la fisica classica, che riprendono l'idea
della quantizzazione: non più solo oscillatori armonici
però, e non solo dell'energia! Dagli sviluppi ulteriori
del modello di Bohr (vecchia teoria dei quanti) nascerà
poi la meccanica quantistica vera e propria.
Relatività speciale e generale
A completare il quadro delle innovazioni di inizio '900 c'è
poi la relatività di Einstein. Della relatività qui
non parliamo in dettaglio, sia perché, a differenza dei
temi appena esposti, è alquanto slegata dalla termodinamica,
sia perché essa era argomento degli incontri tenuti
l'anno scorso in questa stessa sede. Qui ci limitiamo a notare che,
malgrado quel che si è portati a credere, l'impatto
della relatività einsteiniana nella fisica degli inizi
del '900 non è stato affatto immediato. La teoria
non aveva creato lacerazioni evidenti (non nella fisica almeno) e
i fisici si abituarono un po' alla volta ad accettarla, aspettando
qualche anno prima di avere verifiche sperimentali. Valga a titolo
di esempio l'atteggiamento di Planck, espresso in un saggio del
1925 (E. Planck, A Survay of
Physical Theory, Dover Publ., 1993): "[...] Ma quei fisici
sperimentali che hanno la loro mente libera da pregiudizi non si
oppongono per nulla alla teoria della relatività. Al momento,
essi lasciano che le cose procedano quietamente e rimangono in
attesa di risultati che possano dimostrarne sperimentalmente la
validità."
|
2. L'arma del delitto
Secondo la riscostruzione appena proposta, ma anche molte altre,
il punto di svolta tra fisica classica e fisica moderna
è individuabile nello studio della radiazione di corpo nero.
In estrema sintesi, si dice che la fisica classica era incapace di
predire il comportamento osservato della radiazione di corpo nero, dato
che il suo massimo risultato era la legge di Rayleigh-Jeans. A partire
dal fallimento di quest'ultima, Planck introdusse nuove ipotesi, arrivando
così alla formula giusta.
L'ipotesi centrale era la quantizzazione
dell'energia. In pratica, Planck usò uno
spettro discreto di energie anziché continuo, e ciò bastava
per dare predizioni in accordo con gli esperimenti. Su questa idea si
innestarono poi le idee di Einstein (effetto fotoelettrico e calori
specifici) e gli sviluppi successivi della
fisica quantistica.
Dunque, la principale arma del
delitto compiuto ai danni della fisica classica,
è la formula di Planck per
la radiazione di corpo nero.
3. Gli indizi dimenticati
Ci sono però varie cose che non tornano:
La formula di Planck non ha fatto alcun clamore, né
nell'anno della sua pubblicazione, il 1900, né in vari
anni successivi. Ora, se la misura dell'emissione di corpo nero
è l'esperimento cruciale che permette la falsificazione
della vecchia teoria e la nascita di una nuova teoria, ebbene,
ci aspetteremmo che la comunità dei fisici si rendesse conto
rapidamente di questo evento. C'è il delitto e c'è
pure l'arma! Dato che questo non è avvenuto, sarà
opportuno ricercarme le ragioni. Una di queste sta nel fatto che
il dibattito principale non era attorno al corpo nero, ma
era spostato altrove: c'erano fenomeni ritenuti più
importanti e intriganti, come le scoperte sui raggi catodici, sui
raggi X e sulla radioattività, e già questi
davano grattacapi terribili. I lavori di Planck sul corpo nero
(ne aveva già scritti 6 in soli tre anni, prima di quello
sulla discretizzazione dell'energia) non erano dunque al centro
della ribalta. A prova di ciò basti dire che
Henri Poincaré, uno dei più illustri fisici-matematici
dell'epoca, scrisse due libri fondamentali tra il 1902 e il 1905,
"La Science et l'Hypothèse", "La Valeur de la Science",
fornendo un'ampia panoramica sui problemi della scienza in generale
e della fisica in particolare, senza citare mai il problema della
radiazione di corpo nero e il nome di Planck. Fino al 1905, se
anche qualcuno notò il lavoro di Planck, lo fece senza
accorgersi che conteneva ipotesi in netto contrasto con le teorie
classiche. E se non bastasse, lo stesso Planck non sembrò dare
importanza alle conseguenze del suo lavoro e non scrisse null'altro
sull'argomento almeno fino al 1906. Rimase convinto, finché gli
eventi non lo convinsero del contrario, che la discretizzazione
dell'energia fosse una specie di artificio matematico, per nulla legato
al comportamento reale dei processi di assorbimento ed emissione
di radiazione da parte della materia. Per questo motivo non interpretava
il suo lavoro come una rottura con la fisica classica. Cominciò
a pensarlo solo dal 1908, sostenuto dal lavoro di H. Lorentz. Prima di allora,
fu Einstein nel 1905 a scrivere il lavoro sull'effetto
fotoelettrico in cui riconosceva esplicitamente l'importanza delle
nuove ipotesi di Planck sulla quantizzazione dell'energia.
La legge di Rayleigh-Jeans non è antecedente a quella
di Planck. Prima di Planck
la fisica classica non aveva alcuna risposta al problema del
corpo nero, almeno non in termini di modelli microscopici. Lord
Rayleigh discusse la questione del corpo nero in un breve articolo
del 1900, in cui esponeva alcune idee in forma alquanto
dubitativa, riferendosi ai problemi che si incontrano applicando
l'equipartizione dell'energia, nello spirito di Maxwell-Boltzmann,
ad un insieme di oscillatori. A quell'epoca, come già detto
sopra, Planck aveva
scritto ben 6 lavori sulla radiazione del corpo nero, dal 1897 al
1900. La differenza tra i due non è certo nel fatto che
l'uno arriva ad una predizione "sbagliata" e l'altro a quella
"giusta" (il problema era aperto, e non era evidente chi avesse
ragione). Piuttosto, si può dire che Lord
Rayleigh partiva da un atteggiamento positivo rispetto alle
teorie boltzmanniane, ma riconosceva che queste avevano serie
difficoltà (e infatti, il suo lavoro sul corpo nero era
motivato da una critica di Kelvin alla teoria di Maxwell-Boltzmann,
di cui parleremo dopo). Al contrario, Planck partiva da un atteggiamento
ostile nei confronti delle teorie di Boltzmann, per poi
abbracciarle in pieno, quasi forzato dai risultati interessanti a
cui queste lo portavano a dispetto degli sforzi fatti per procedere
in altro modo. Entrambi mostravano dove si potesse arrivare con
le teorie di Boltzmann, ma l'uso di queste non era affatto assodato.
Dire che la fisica classica arrivava solo a Rayleigh-Jeans, mentre
Planck spinse la teoria oltre la soglia della fisica moderna, è
dunque una forzatura. Lo è se si considera
la reale scansione dei tempi,
tanto più che la formula di Rayleigh-Jeans non era
contenuta nell'articolo di Lord Rayleigh del 1900, ma in un
successivo articolo, scritto assieme a Jeans, nel 1905. Ma
soprattutto, lo è perchè la maggior parte dei
fisici "classici" dell'epoca trovavano assai criticabili sia
l'approccio di Rayleigh-Jeans, basato su un principio di
equipartizione di cui ci si fidava poco, sia quello di Planck, basato
su leggi statistiche altrettanto sospette. Nemmeno Planck riteneva
corretto dedurre predizioni dal principio di equipartizione, e
per questo motivo egli stesso ignorò il risultato di
Rayleigh-Jeans.
La discretizzazione introdotta da Planck non era nuova. La usava
spesso Boltzmann nei suoi calcoli di meccanica statistica, come
metodo efficace per semplificare i calcoli. Planck la usò
più o meno nello stesso spirito. A supporto di questo argomento
citiamo un passaggio di Cercignani (C. Cercignani, Ludwig Boltzmann
e la Meccanica Statistica, 1997) a proposito di un lavoro di
Boltzmann del 1872 sulla teoria cinetica dei gas: "[...] Il lavoro
prosegue con una derivazione alternativa basata su un modello a
energie discrete, in modo che l'equazione integro-differenziale
per la funzione di distribuzione diventa un sistema di equazioni
differenziali ordinarie. L'uso di energie discrete è sempre
sembrato a Boltzmann molto più chiaro e intuitivo. [...]
Molti storici della scienza hanno sottolineato il fatto che questi
modelli discreti di Boltzmann guidarono Planck alla scoperta dei
quanti di energia, come Planck stesso riconobbe." Dunque, se la
formula di Planck fu l'arma del delitto, si intravede qui un
possibile motivo per cui il delitto stesso non fu riconosciuto:
Planck non aveva inventato la discretizzazione dell'energia, si
era "solo" accorto che tale discretizzazione, se si voleva riprodurre
l'andamento corretto dell'emissione di corpo nero, non poteva essere
eliminata a posteriori con un passaggio al limite, mandando a zero
il "quanto di energia", ma al contrario bisognava fissare tale "quanto"
alla frequenza della radiazione. Coloro che, all'epoca, si sono limitati
a leggere la prima parte di questo schema (la discretizzazione), non
hanno visto nulla di veramente nuovo. Pochi hanno capito invece
le implicazioni della seconda parte (l'impossibilità di passare
dal discreto al continuo). Nemmeno Planck riuscì a trarre da
tali implicazioni gli elementi per formulare una nuova teoria. E con
questo abbiamo spuntato l'arma, e abbiamo trovato nuovi indizi che
portano a Boltzmann.
La vera novità nel calcolo di Planck è il fatto di
essersi concentrato sull'entropia e di averla calcolata seguendo il
metodo statistico di Boltzmann. Planck si
era convinto che i metodi di Boltzmann erano buoni, pur partendo da
un atteggiamento iniziale di forte critica, ... forse proprio per
questo.
(da Helge Kragh,
Max Planck: the reluctant revolutionary,
Physics World, December 2000)
|
Sono passati 100 anni da quando Max Planck pubblicò
l'articolo che diede vita alla meccanica quantistica - o almeno
questo si racconta. La storia vera, tuttavia, rivela che Planck non
comprese subito le conseguenze del suo lavoro
e divenne un rivoluzionario contro la sua volontà.
Secondo la storia che si racconta abitualmente, e
che sfortunatamente si trova ancora in
molti libri di testo, la meccanica quantistica emerse quando
ci si rese conto che la fisica classica prediceva una distribuzione
di energia per la radiazione del corpo nero in netto contrasto con
le osservazioni sperimentali. La storia continua dicendo che, negli
ultimi anni dell'800, il fisico tedesco Wilhelm Wien derivò
un'espressione che si accordava ragionevolmente bene ai dati empirici -
ma senza alcuna base teorica soddisfacente. Poi, quando Lord Rayleigh
e James Jeans analizzarono di nuovo la radiazione di corpo
nero dal punto di vista della fisica classica, lo spettro che ne
risultò differiva drasticamente sia dalla legge di Wien che
dagli esperimenti. Posto di fronte a questa grave anomalia, Max
Planck si mise in cerca di una soluzione, e nel fare questo fu
forzato ad introdurre la nozione di "quanto d'energia". Con l'ipotesi
dei "quanti" si ottenne un perfetto accordo tra teoria ed
esperimenti. Voila! La teoria dei quanti nasce così.
Questa storia è un mito, più simile ad una favola che
alla verità storica. La meccanica quantistica non deve le sue origini
ad alcun fallimento della fisica classica, ma piuttosto al fatto che
Planck conosceva profondamente la termodinamica.
|
In conclusione,
la riscostruzione iniziale, sintetica e semplificata, non regge
ai nuovi indizi. Bisogna allargare lo sguardo attorno al delitto,
fiutando nuove piste d'indagine. Ci si guarda attorno e si
scruta meglio l'ambiente che fa da cornice all'evento. Chi si
muoveva là attorno?
|




 Effetto fotoelettrico
Effetto fotoelettrico Calore specifico dei solidi
Calore specifico dei solidi