|
La termodinamica: dal macroscopico al microscopico
|



|
Moventi e cambiamenti
1. Boltzmann: dalla meccanica analitica alle leggi statistiche
Si parte con un programma e se ne realizza un altro. Boltzmann inizia
il suo lavoro con l'obiettivo di elaborare una prova puramente
analitica del secondo principio della termodinamica, e finisce
per elaborare una teoria fondamentalmente statistica.
(da Enrico Bellone, Il mondo di carta, Mondadori 1976)
|
Nei primi scritti sulla teoria cinetica dei gas il progetto
boltzmanniano è indubbiamente un progetto fortemente
riduzionistico, nel senso che imposta la matematizzazione della teoria
con il fine esplicito di ridurla ad un capitolo della meccanica
razionale. Ma già nelle memorie del 1871 si assiste ad uno
spostamento significativo all'interno di quel progetto. Boltzmann
era infatti partito con l'intenzione di elaborare una prova
"puramente analitica" del secondo principio della termodinamica e,
nel 1866, aveva preteso di trasformare quel principio in un "assioma
di meccanica pura": a suo avviso era valido sostenere che il
principio in questione corrispondeva al principio di minima azione.
Nel 1871, tuttavia, Boltzmann riesaminava quel progetto in modo
globale, introducendo nella teoria, in forme sempre più
radicali, nozioni e inferenze basate sul calcolo delle probabilità.
Questa revisione approdava, nel 1872, in una monumentale monografia
con la quale Boltzmann prendeva le distanze sia dalle proprie
precedenti ricerche, sia da quelle che, negli stessi anni, erano
perseguite da Maxwell, Clausius e Szily. Il problema non era più
quello di trovare delle catene deduttive che fossero in grado di eliminare
la posizione eccezionale del secondo principio riducendo quest'ultimo
alla meccanica: si doveva invece spiegare il secondo principio
attraverso una sottilissima analisi dei rapporti esistenti tra esso
e il calcolo delle probabilità.
|
Nel lungo articolo del 1872, Boltzmann affronta il problema
dell'irreversibilità usando, esplicitamente e per la prima
volta, argomenti probabilistici. Introdusse una definizione di entropia
in termini di velocità molecolari e dimostrò che
questa quantità deve sempre crescere, o, al più,
restare costante (in condizioni di equilibrio). Ricavò anche
l'equazione, poi detta equazione di Boltzmann, per le funzioni
di distribuzione delle posizioni e delle velocità delle
molecole di un gas. Infine, dimostrò che la derivata rispetto
al tempo di una quantità, H, opportunamente definita, non
è mai positiva, ed è nulla solo se la distribuzione
delle velocità coincide con quella di Maxwell. Questo
è noto come il "teorema H". L'equazione di Boltzmann e il
teorema H, presentati nella memoria del 1872, ebbero effetti
contrastanti: da una parte l'equazione venne applicata con successo
a molti fenomeni fisici, dall'altra le idee di Boltzmann suscitarono
reazioni e critiche, anche aspre, da parte di colleghi fisici e
matematici. Due critiche importanti furono presentate in forma di
paradossi: 1) il paradosso di reversibilità di Loschmidt
(ovvero, l'invarianza delle equazioni del moto per inversione del
segno del tempo usata come argomento per negare validità
alle spiegazioni meccaniche del secondo principio della
termodinamica; argomento suggerito e sostenuto da Lord Kelvin),
2) il paradosso della ricorrenza di Zermelo (ovvero, il fatto
che un mondo limitato, governato solo dalle leggi della meccanica,
passerà per ogni stato vicino a quello iniziale; si tratta
di un argomento basato su un teorema di Poincaré, il quale
pensava, tra l'altro, che "la concezione meccanicistica del mondo
ha sedotto tante brave persone").
Quando questi paradossi apparirono sulla scena (intorno al 1874-76
il primo, e nel 1896 il secondo) Boltzmann aveva già convertito
il suo programma da "analitico" a "probabilistico". Ma la risposta
a Loschmidt rappresenta un ulteriore passo in quella direzione,
facendogli prendere atto pienamente della natura probabilistica
del secondo principio ("[...] questo risultato è una
conseguenza della teoria della probabilità, in quanto
ogni distribuzione disuniforme di stati, per quanto improbabile,
non è assolutamente impossibile... [...] Il numero di
stati che portano a distribuzioni uniformi dopo un certo tempo t
è molto più grande di quello degli stati che portano
a distribuzioni disuniformi..."). E nella risposta a Zermelo,
Boltzmann afferma che "non si stava parlando di una spiegazione
meccanica del secondo principio, ma anzi di una sua delimitazione
ad affermazione non assolutamente certa, ma improbabile. [...]
Quando il Sig. Zermelo conclude, dal fatto teorico che gli stati
iniziali devono ripresentarsi - senza aver calcolato quanto
tempo questo richiederà -, che le ipotesi della teoria dei
gas devono essere abbandonate, egli è come il giocatore
di dadi che ha calcolato che non è nulla la probabilità
di una successione di mille 'uno' e allora conclude che un dado
è truccato perché non ha mai osservato una tale
successione!"
(da M. Planck, The Unity of the Physical Universe, in
A Survay of Physical Theory,
Dover Publ., 1993; prima edizione 1925)
Per completare l'emancipazione del concetto di entropia dalle procedure
sperimentali umane, e quindi stabilire un vero principio alla base della
seconda legge [della termodinamica], ci volle il lavoro ("life-work")
di Ludwig Boltzmann. In breve esso consiste nel rendere il concetto di
entropia dipendente da quello di probabilità. Così si
dà significato alla predilezione della Natura per
certi stati. La Natura preferisce stati più probabili
rispetto a quelli meno probabili, così che tutti i processi
tendono spontaneamente alla formazione di stati aventi grande
probabilità. Il calore fluisce da un corpo a temperatura più
alta verso un corpo a temperatura più bassa, perché lo
stato in cui la temperatura dei due corpi è uguale è
più probabile di quello in cui le temperature sono diverse.
Il calcolo di una certa misura della probabilità per ogni
stato di un sistema è stato reso possibile
dall'introduzione della teoria degli atomi, e di metodi statistici.
|
(da M. Planck, Dynamical Laws and Statistical Laws, in
A Survay of Physical Theory,
Dover Publ., 1993; prima edizione 1925)
|
L'irreversibilità di tutti i processi naturali costituì un
serio problema per la concezione meccanica, dato che in meccanica tutti
i processi sono reversibili. Fu necessaria l'analisi sistematica e
l'inflessibile ottimismo di un Ludwig Boltzmann non solo per
riconciliare la teoria degli atomi con la seconda legge della
termodinamica, ma anche per spiegare per la prima volta il
significato fondamentale della seconda legge sulla base della
teoria degli atomi.
|
(da Henri Poincaré, La Valeur de la Science, Champs-
Flammarion, 1970; prima edizione 1905)
|
Ecco dunque quale sarebbe il tipo di fenomeno fisico irreversibile:
nascondere un chicco d'orzo in un sacco pieno di grano è
facile; ritrovarlo in seguito e estrarlo dal sacco è
praticamente impossibile. Tutto questo c'è stato spiegato
da Boltzmann e Maxwell [...].
|
|
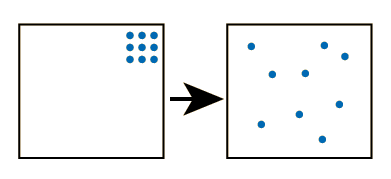
S = k log W

|
2. Planck: dall'energia agli atomi
Si parte con un programma e se ne realizza un altro. Planck inizia
il suo lavoro con l'obiettivo di mostrare che l'ipotesi atomistica
è incompatibile con il secondo principio della termodinamica,
e finisce per aderire alle leggi statistiche di Boltzmann, diventando,
quasi inconsapevolmente, l'apripista delle moderne teorie degli atomi.
(da Helge Kragh,
Max Planck: the reluctant revolutionary,
Physics World, December 2000)
|
[...] Planck was
appointed professor of physics at the University of Berlin in 1889. His
doctoral dissertation from the University of Munich dealt with the second
law, which was also the subject of most of his work until about 1905.
Planck's thoughts centred on the concept of entropy and how to understand
"irreversibility" on the basis of the absolute validity of the entropy law -
the version of the second law of thermodynamics formulated in terms of the
entropy concept.
In the 1890s the debate about the second law centred on the statistical (or
probabilistic) interpretation that Ludwig Boltzmann had originally proposed
back in 1872 and expanded in 1877. According to Boltzmann's
molecular-mechanical interpretation, the entropy of a system is the
collective result of molecular motions. The second law is valid only in a
statistical sense. Boltzmann's theory, which presupposed the existence of
atoms and molecules, was challenged by Wilhelm Ostwald and other
"energeticists", who wanted to free physics from the notion of atoms and
base it on energy and related quantities.
What was Planck's position in this debate? One might expect that he sided
with the winners, or those who soon turned out to be the winners - namely
Boltzmann and the "atomists". But this was not the case. Planck's belief in
the absolute validity of the second law made him not only reject Boltzmann's
statistical version of thermodynamics but also doubt the atomic hypothesis
on which it rested. As early as 1882, Planck concluded that the atomic
conception of matter was irreconcilably opposed to the law of entropy
increase. "There will be a fight between these two hypotheses that will
cause the life of one of them," he predicted. As to the outcome of the
fight, he wrote that "in spite of the great successes of the atomistic
theory in the past, we will finally have to give it up and to decide in
favour of the assumption of continuous matter".
However, Planck's opposition to atomism waned during the 1890s as he
realized the power of the hypothesis and the unification it brought to a
variety of physical and chemical phenomena. All the same, his attitude to
atomism remained ambiguous and he continued to give priority to macroscopic
thermodynamics and ignore Boltzmann's statistical theory. Indeed, by 1895 he
was ready to embark on a major research programme to determine thermodynamic
irreversibility in terms of some micro-mechanical or micro-electrodynamical
model that did not explicitly involve the atomic hypothesis.
|
(da C. Cercignani, Ludwig Boltzmann e la meccanica statistica,
Percorsi della Fisica, La Goliardica Pavese, 1997)
|
Dopo aver pubblicato un lavoro in cinque parti tra gli anni 1896 e 1899
sulla radiazione del corpo nero, Planck presentò le sue conclusioni
in un ulteriore lavoro dallo stesso titolo, apparso nel 1900.
Inizialmente impressionato dal paradosso di Zermelo, scrive: "Senza dubbio,
la teoria cinetica ha affrontato il compito di spiegare la tendenza
all'equilibrio termomeccanico [...] in termini di effetti conservativi, cioè
come il risultato finale di tutti gli urti tra le numerose molecole che,
concepite come atomi, interagiscono attraverso forze conservative. Ma uno
studio più accurato fa vedere che i moti molecolari supposti
dalla teoria cinetica dei gas non sono in nessun senso unidirezionali, e che,
in modo del tutto generale, qualsiasi stato sia esistito una volta, nel
corso del tempo si verificherà con una frequenza così
elevata da soddisfare qualsiasi livello desiderabile di approssimazione.
Partendo dal punto di vista della teoria cinetica dei gas non si otterrà
alcuna rigorosa teoria della viscosità se non si ricorre a qualche
ipotesi addizionale"
[...] Credo di dover riconoscere come processo unidirezionale, costituito
da effetti completamente conservativi, l'influenza di un risuonatore
che vibra senza attrito o resistenza sull'onda che lo eccita...". Infatti,
tale risuonatore avrebbe alterato il campo, per esempio assorbendo
energia da un'onda piana e riemettendola sotto forma di onda sferica
oppure eliminando gradualmente le fluttuazioni o anche alterando lo
spettro. Inoltre, essendo il sistema a inifiniti gradi di libertà
(in quanto include il campo), il paradosso di Zermelo sarebbe stato evitato.
Nelle prime tre parti del suo lavoro, Planck prosegue su questa linea
(che potremmo definire anti-boltzmanniana). [...]
Quattro mesi dopo la presentazione della prima parte del lavoro di
Planck, venne illustrata, alla stessa Accademia di Berlino, una breve
critica di Boltzmann, che rilevava, dopo il riconoscimento del grande
valore delle formule ricavate da Planck, come il programma per cui esse
erano state sviluppate fosse destinato a fallire. Infatti, il paradosso
della reversibilità (ben familiare a Boltzmann) restava pienamente
valido. Senza invocare condizioni iniziali opportune (anche se altamente
probabili) non si poteva dedurre un'equazione irreversibile da equazioni
reversibili.
[...]
Con la quarta parte delle sue comunicazioni all'Accademia, il programma
di Planck cambia completamente [...]. Quel che è certo è
che, ben prima d'introdurre l'ipotesi del quanto di energia nel 1900,
Planck si era convertito alle idee della teoria cinetica, [...] aveva
adottato una linea boltzmanniana.
|
(da M. Planck, Nobel Lecture, Stoccolma, 1920)
|
[...] my hypothesis that the resonator
could exercise a unilateral, i.e. irreversible, effect upon the
energy in the surrounding radiation field, was strongly contested
by Ludwig Boltzmann, who, with his riper experience in these problems,
proved that according to the laws of classical dynamics each of
the processes observed by me can proceed in exactly the opposite
direction, in such a way, that a spherical wave emitted from the
resonator, returns and contracts in steadily diminishing concentric
spherical surfaces inwards to the resonator, and is again absorbed
by it, thereby allowing the formerly absorbed energy to be re-transmitted
into space in the direction from which it came. And when I excluded
this kind of singular process, such as an inwardly directed wave,
by means of the introduction of a limiting definition, the hypothesis
of natural radiation, all these analyses still showed ever more
clearly that an important connecting element or term, essential
for the complete grasp of the core of the problem, must be missing.
So there was nothing left for me but to tackle
the problem from the opposite side, that of thermodynamics, in which
field I felt, moreover, more confident. In fact my earlier studies
of the Second Law of Heat Theory stood me in good stead, so that
from the start I tried to get a connection, not between the temperature
but rather the entropy of the resonator and its energy, and in fact,
not its entropy exactly but the second derivative with respect to
the energy since this has a direct physical meaning for the irreversibility
of the energy exchange between resonator and radiation. [...]
[...] this
problem led me automatically to a consideration of the connection
between entropy and probability, that is, Boltzmann's trend of ideas;
until after some weeks of the most strenuous work of my life, light
came into the darkness, and a new undreamed-of perspective opened
up before me.
[...] In a similar way to that for energy, an absolute
value can be defined also for entropy and, as a result thereof,
for the physical probability too, e.g. by so fixing the additive
constant that energy and entropy disappear together. On the basis
of a consideration of this kind a specific, relatively simple combinatorial
method was obtained for the calculation of the physical probability
of a specified energy distribution in a system of resonators, which
led exactly to that entropy expression determined by the radiation
law, and it brought me much-valued satisfaction for the many disappointments
when Ludwig Boltzmann, in the letter returning my essay, expressed
his interest and basic agreement with the train of thoughts expounded
in it.
|
3. I percorsi tortuosi della scienza
A questo punto, il nostro investigatore non può trattenere
una smorfia di disappunto. Gli avevano detto che sarebbe stato un
caso semplice, che la scienza procede dritta dritta verso
scopi precisi, che basta solo trovare la pista che porta dalla
congettura iniziale, all'esperimento, alla teoria e così
di seguito. Invece no! La storia della scienza è davvero complicata
e gli intrecci attorno ad ogni evento, ogni esperimento, ogni
nuova teoria, sono intricati. Ora, nel libretto dell'investigatore
ci sono troppe apparenti contraddizioni. Ci sono due scienziati
che stravolgono la fisica con i loro studi. Ciascuno di essi realizza
progetti avendone preventivati altri, opposti. Uno di essi, Boltzmann,
propone una nuova teoria basata su leggi statistiche con una forte
carica innovativa, attirandosi le critiche aspre di molti colleghi,
ma lo fa sentendosi un reazionario ("Indeed, when
I look back on all these developments and revolutions I feel like
a monument of ancient scientific memories. I would go further and
say that I am the only one left who still grasped the old doctrines
with unreversed enthusiasm - at any rate I am the only one who still
fights for them as far as he can. [...]. I therefore present
myself to you as a reactionary, one who has stayed behind and
remains enthusiastic for the old classical doctrines as against the
men of today."). L'altro, Planck, introduce ipotesi rivoluzionarie,
ma quasi senza accorgersene, senza fare troppo rumore, senza trarne
tutte le conseguenze. Sarebbero loro ad aver progettato ed eseguito il
delitto ai danni della fisica classica? Fosse stato per loro, pensa
l'investigatore, la fisica classica non sarebbe mai morta... Ma è
davvero morta?
|




